题目内容
△ABC中acosA=bcosB时，三角形的形状是（ ）
| A、正三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、前面说法都错 |
考点：三角形的形状判断
专题：解三角形
分析：由acosA=bcosB，利用余弦定理可得：a×
=b×
，可得a=b或a2+b2=c2．即可判断出．
| b2+c2-a2 |
| 2bc |
| a2+c2-b2 |
| 2ac |
解答：
解：∵acosA=bcosB，
∴a×
=b×
，
化为（a2-b2）（a2+b2-c2）=0，
∴a=b或a2+b2=c2．
∴三角形是等腰三角形或直角三角形．
因此A，B，C的说法都不全面．
故选：D．
∴a×
| b2+c2-a2 |
| 2bc |
| a2+c2-b2 |
| 2ac |
化为（a2-b2）（a2+b2-c2）=0，
∴a=b或a2+b2=c2．
∴三角形是等腰三角形或直角三角形．
因此A，B，C的说法都不全面．
故选：D．
点评：本题考查了利用余弦定理判定三角形的形状，属于基础题．
练习册系列答案
相关题目
若数列{an}的前n项和为Sn=
an+
，则数列{an}的通项公式为（ ）
| 2 |
| 3 |
| 1 |
| 3 |
| A、an=-2n-1 |
| B、an=（-2）n-1 |
| C、an=（-2）n |
| D、an=-2n |
若函数h（x）=2x-k（
+1）在（1，+∞）上是增函数，则实数k的取值范围是（ ）
| 1 |
| x |
| A、[-2，+∞） |
| B、[2，+∞） |
| C、（-∞，-2] |
| D、（-∞，2] |
函数f（x）的定义域为R，f（-1）=2，对任意x∈R，f′（x）＞2，则f（x）＞2x+4的解集为（ ）
| A、（一1，1） |
| B、（一1，+∞） |
| C、（一∞，一1） |
| D、（一∞，+∞） |
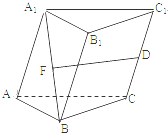在三棱柱ABC-A1B1C1中，D是CC1的中点，F是A1B的中点，且| DF |
| AB |
| AC |
A、α=
| ||
B、α=-
| ||
C、α=1，β=-
| ||
D、α=-1，β=
|
若-2π＜α＜-π，化简
+
得（ ）
|
|
A、-
| ||||||
B、
| ||||||
C、-
| ||||||
D、
|
对于线性相关系数r，下列说法正确的是（ ）
| A、|r|∈（-∞，+∞），|r|越大，相关程度越大；反之，相关程度越小 |
| B、|r|≤1，r越大，相关程度越大；反之，相关程度越小 |
| C、|r|≤1，且|r|越接近于1，相关程度越大；|r|越接近于0，相关程度越小 |
| D、以上说法都不正确 |
在锐角三角形中，a、b、c分别是内角A、B、C的对边，设B=2A，则
的取值范围是（ ）
| b |
| a |
| A、（-2，2） | ||||
| B、（0，2） | ||||
C、（
| ||||
D、（
|