题目内容
14．已知m，n为异面直线，m∥平面α，n∥平面β，α∩β=l，则l（ ）| A． | 与m，n都相交 | B． | 与m，n中至少有一条相交 | ||
| C． | 与m，n都不相交 | D． | 与m，n中一条相交 |
分析 假设l与m相交，则m与α有公共点，得出矛盾，同理推出l与n的关系．
解答 解：假设l与m相交，交点为P，则m与α有公共点P，与m∥α矛盾，
故l与m不相交，同理可得：l与n不相交．
故选：C．
点评 本题考查了空间线面的位置关系，属于基础题．
练习册系列答案
相关题目
4．已知数列{an}满足a1=1，a2=2，an+2-an=3，则当n为偶数时，数列{an}的前n项和Sn=（ ）
| A． | $\frac{{3{n^2}}}{8}$-$\frac{1}{4}$ | B． | $\frac{{3{n^2}}}{8}$+$\frac{1}{4}$ | C． | $\frac{{3{n^2}}}{4}$ | D． | $\frac{{3{n^2}}}{8}$ |
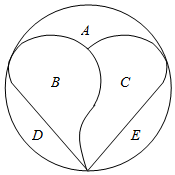如图所示，积木拼盘由A、B、C、D、E五块积木组成，若每块积木都要涂一种颜色，且为了体现拼盘的特色，相邻的区域需涂不同的颜色（如：A与B为相邻区域，A与D为不相邻区域），现有五种不同的颜色可供挑选，则可组成的不同的积木拼盘的种数是（ ）