题目内容
6．在等差数列{an}中，a4+a7+a10+a13=20．则S16=40．分析 利用等差数列的通项公式、前n项和公式求解．
解答 解：∵在等差数列{an}中，a4+a7+a10+a13=2（a1+a16）=20，
∴S16=$\frac{16}{2}（{a}_{1}+{a}_{16}）$=$\frac{16}{2}×\frac{10}{2}$=40．
故答案为：40．
点评 本题考查数列的前16项和的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
17．
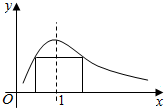一矩形的一边在x轴上，另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$（x＞0）的图象上，如图，则此矩形绕x轴旋转而成的几何体的体积的最大值是（ ）
一矩形的一边在x轴上，另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$（x＞0）的图象上，如图，则此矩形绕x轴旋转而成的几何体的体积的最大值是（ ）| A． | π | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
14．已知m，n为异面直线，m∥平面α，n∥平面β，α∩β=l，则l（ ）
| A． | 与m，n都相交 | B． | 与m，n中至少有一条相交 | ||
| C． | 与m，n都不相交 | D． | 与m，n中一条相交 |
1．下列说法中错误的是（ ）
| A． | 零向量平行于任何向量 | |
| B． | 对于平面上意三点A，B，C，一定有$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | |
| C． | 若$\overrightarrow{AB}$=m$\overrightarrow{CD}$（m∈R），则$\overrightarrow{AB}$∥$\overrightarrow{CD}$ | |
| D． | 若$\overrightarrow{a}$=m$\overrightarrow{i}$，$\overrightarrow{b}$=n$\overrightarrow{j}$，则当m=n时，$\overrightarrow{a}=\overrightarrow{b}$ |
15．三角形ABC的三个内角A，B，C成等差数列，AC=3，cosC=$\frac{\sqrt{6}}{3}$，则AB=（ ）
| A． | 2$\sqrt{2}$ | B． | 8 | C． | 2 | D． | 4 |