题目内容
4.已知数列{an}满足a1=1,a2=2,an+2-an=3,则当n为偶数时,数列{an}的前n项和Sn=( )| A. | $\frac{{3{n^2}}}{8}$-$\frac{1}{4}$ | B. | $\frac{{3{n^2}}}{8}$+$\frac{1}{4}$ | C. | $\frac{{3{n^2}}}{4}$ | D. | $\frac{{3{n^2}}}{8}$ |
分析 数列{an}满足a1=1,a2=2,an+2-an=3,可知:此数列的奇数项与偶数项分别成等差数列,公差都为3,利用等差数列的通项公式及其前n项和公式即可得出.
解答 解:数列{an}满足a1=1,a2=2,an+2-an=3,
可知:此数列的奇数项与偶数项分别成等差数列,公差都为3,
且a2k-1=1+3(k-1)=3k-2,a2k=2+3(k-1)=3k-1.
则当n为偶数时,设2k=n,数列{an}的前n项和Sn=$\frac{k(1+3k-2)}{2}$+$\frac{k(2+3k-1)}{2}$=3k2=$\frac{3}{4}{n}^{2}$.
故选:C.
点评 本题考查了等差数列的通项公式及其前n项和公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
14.若变量x、y满足约束条件$\left\{\begin{array}{l}{x+2y≤2}\\{x+y≥0}\\{x≤4}\end{array}\right.$则z=4x+y的最大值为( )
| A. | -8 | B. | 10 | C. | 12 | D. | 15 |
15.在复平面内,复数$\frac{1-2i}{2+i}$对应的点的坐标为( )
| A. | ($\frac{4}{5}$,$\frac{3}{5}$) | B. | ($\frac{4}{5}$,-$\frac{3}{5}$) | C. | (0,1) | D. | (0,-1) |
12.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为( )

| A. | 96 | B. | $80+4\sqrt{2}π$ | C. | $96+4(\sqrt{2}-1)π$ | D. | $96+4(2\sqrt{2}-1)π$ |
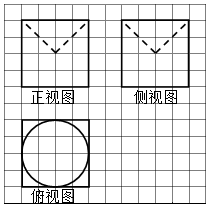
9.已知某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{8π}{3}$ | B. | 3π | C. | $\frac{10π}{3}$ | D. | $\frac{11π}{3}$ |
14.已知m,n为异面直线,m∥平面α,n∥平面β,α∩β=l,则l( )
| A. | 与m,n都相交 | B. | 与m,n中至少有一条相交 | ||
| C. | 与m,n都不相交 | D. | 与m,n中一条相交 |
