题目内容
2．求y=$\frac{{x}^{2}+8x+11}{{x}^{2}+7x+10}$（x＞-1）最大值．分析 化简y=$\frac{{x}^{2}+8x+11}{{x}^{2}+7x+10}$=1+$\frac{x+1}{（x+2）（x+5）}$，换元x+1=t，t＞0；从而可得y=1+$\frac{1}{t+\frac{4}{t}+5}$，从而利用基本不等式求其最值．
解答 解：y=$\frac{{x}^{2}+8x+11}{{x}^{2}+7x+10}$
=1+$\frac{x+1}{{x}^{2}+7x+10}$
=1+$\frac{x+1}{（x+2）（x+5）}$，
令x+1=t，t＞0；
则y=1+$\frac{t}{（t+1）（t+4）}$=1+$\frac{1}{t+\frac{4}{t}+5}$，
∵t+$\frac{4}{t}$≥4，
（当且仅当t=$\frac{4}{t}$，即t=2，x=1时，等号成立），
∴1+$\frac{1}{t+\frac{4}{t}+5}$≤1+$\frac{1}{9}$=$\frac{10}{9}$，
故y=$\frac{{x}^{2}+8x+11}{{x}^{2}+7x+10}$（x＞-1）的最大值为$\frac{10}{9}$．
点评 本题考查了学生的化简运算能力及基本不等式在求最值中的应用，同时考查了换元法的应用．
练习册系列答案
阅读快车系列答案
相关题目
12．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为（ ）
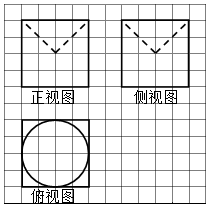
| A． | 96 | B． | $80+4\sqrt{2}π$ | C． | $96+4（\sqrt{2}-1）π$ | D． | $96+4（2\sqrt{2}-1）π$ |
17．
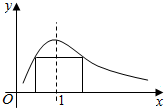一矩形的一边在x轴上，另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$（x＞0）的图象上，如图，则此矩形绕x轴旋转而成的几何体的体积的最大值是（ ）
一矩形的一边在x轴上，另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$（x＞0）的图象上，如图，则此矩形绕x轴旋转而成的几何体的体积的最大值是（ ）| A． | π | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
7．从1、2、3、4、5这5个数中随机取出一个数，取出的数是某个整数的平方数的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
14．已知m，n为异面直线，m∥平面α，n∥平面β，α∩β=l，则l（ ）
| A． | 与m，n都相交 | B． | 与m，n中至少有一条相交 | ||
| C． | 与m，n都不相交 | D． | 与m，n中一条相交 |