题目内容
16．若单位向量$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$，向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$$+λ\overrightarrow{{e}_{2}}$（λ∈R），且|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{2}$，则λ=（ ）| A． | -$\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$-1 | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
分析 根据向量的数量积的运算和向量的模的计算即可．
解答 解：向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$$+λ\overrightarrow{{e}_{2}}$（λ∈R），且|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{2}$，
∴|$\overrightarrow{a}$|2=|$\overrightarrow{{e}_{1}}$$+λ\overrightarrow{{e}_{2}}$|2=|$\overrightarrow{{e}_{1}}$|2+|λ$\overrightarrow{{e}_{2}}$|2+2λ$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=1+λ2+λ=$\frac{3}{4}$，
解得λ=-$\frac{1}{2}$，
故选：A．
点评 本题考查了向量的数量积的运算和向量的模的计算，属于基础题．
练习册系列答案
相关题目
1．
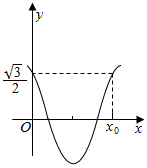已知函数f（x）=2cos（πx）•cos2$\frac{φ}{2}$-sin（πx）•sinφ-cos（πx）（0≤φ＜$\frac{π}{2}$）的部分图象如图所示，则图中的x0的值为（ ）
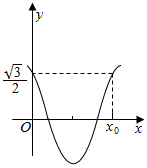已知函数f（x）=2cos（πx）•cos2$\frac{φ}{2}$-sin（πx）•sinφ-cos（πx）（0≤φ＜$\frac{π}{2}$）的部分图象如图所示，则图中的x0的值为（ ）| A． | $\frac{5}{6}$ | B． | $\frac{5}{4}$ | C． | $\frac{5}{2}$ | D． | $\frac{5}{3}$ |
B．
C．
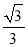D．
