已知θ为锐角.且sinθ:cos$\frac{θ}{2}$=8:5.求sinθcosθ 题目和参考答案——青夏教育精英家教网——

题目内容

7．已知θ为锐角，且sinθ：cos$\frac{θ}{2}$=8：5，求sinθcosθ

分析利用二倍角的正弦函数求出半角的正弦函数，然后求解正弦函数与余弦函数值即可．

解答解：θ为锐角，且sinθ：cos$\frac{θ}{2}$=8：5，
可得sin$\frac{θ}{2}$=$\frac{4}{5}$，cos$\frac{θ}{2}$=$\frac{3}{5}$，
sinθ=2sin$\frac{θ}{2}$cos$\frac{θ}{2}$=$\frac{24}{25}$．
cosθ=$\sqrt{1-si{n}^{2}θ}$=$\frac{7}{25}$．
sinθcosθ=$\frac{168}{625}$．

点评本题考查二倍角的正弦函数以及同角三角函数基本关系式的应用，考查计算能力．

练习册系列答案

世纪百通主体课堂小学课时同步达标系列答案

世纪百通优练测系列答案

世纪百通课时作业系列答案

百分学生作业本题练王系列答案

小学1课3练培优作业本系列答案

中华题王系列答案

优翼学练优系列答案

优加学习方案系列答案

52045模块式全能训练系列答案

钟书金牌新教材全练系列答案

相关题目

2．已知{a_n}（n=1，2，3，…）是由非负整数组成的无穷数列，该数列前n项的最大值记为A，第n项之后各项a_n+1，a_n+2…的最小值记为B_n，d_n=A_n-B_n．
（1）若{a_n}满足a₁=3，当n≥2时，a_n=3ⁿ-1，写出d₁，d₂，d₃的值；
（2）设d是非负整数，证明：d_n=-d的充分必要条件为{a_n}是公差为d的等差数列．

2．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A₁，上顶点为B₂、右焦点为F₂，椭圆C的离心率为$\frac{\sqrt{2}}{2}$，△A₁B₂F₂的面积为$\sqrt{2}$+1．
（1）求椭圆C的方程；
（2）直线1：y=k（x-$\sqrt{2}$），k≠0与椭圆C交于A，B两点，与y轴交于点M，A与C关于y轴对称，直线BC与y轴交于点N．求证：|0M|•|0N|为定值．

18．已知过双曲线C：$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦点的直线1与C交于A，B两点，且使|AB|=4a的直线1恰好有3条，则双曲线C的渐近线方程为（　　）

y=±$\sqrt{2}$x

y=±$\frac{\sqrt{2}}{2}$x

y=±$\frac{1}{2}$x

2．在△ABC中，B=$\frac{π}{3}$，AB=2，D为AB中点，△BCD的面积为$\frac{3\sqrt{3}}{4}$，则AC等于（　　）

12．已知数列{a_n}满足a_n+1=$\sqrt{{a}_{n}^{2}+4}$，且a₁=1，数列b_n=${a}_{n}^{2}$，则{b_n}的前n项和S_n=2n²-n．

19．已知在数列{a_n}中，a₁=2，a_n+1=4a_n+6，n∈N^*
（1）求证：数列{a_n+2}为等比数列；
（2）求数列{（-1）ⁿna_n}的前n项和S_n．

16．若单位向量$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$，向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$$+λ\overrightarrow{{e}_{2}}$（λ∈R），且|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{2}$，则λ=（　　）

$\frac{\sqrt{3}}{2}$-1

$\frac{\sqrt{3}}{2}$

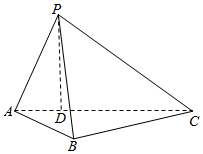如图所示，在三棱锥P-ABC中，$AB=BC=2\sqrt{3}$，平面PAC⊥平面ABC，PD⊥AC于点D，AD=2，CD=4，PD=3．
（1）求三棱锥P-ABC的体积；
（2）证明：△PBC为直角三角形．