题目内容
19.一次测试中,为了了解学生的学习情况,从中抽取了n个学生的成绩(满分为100分)进行统计.按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60),[90,100]的数据).
(1)求样本容量n和频率分布直方图中x,y的值;
(2)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取2名参加志愿者活动,设X表示所抽取的2名同学中得分在[80,90)内的学生人数,求事件“X=2”的概率.
分析 (1)根据频率分布直方图的性质求得样本容量n和频率分布直方图中x、y的值.
(2)由题意可知,分数在[80,90)有4人,分别记为a,b,c,d,分数在[90,100)有2人,分别记为A,B,用列举法求得所有的抽法有15种,而满足条件的抽法有6种,由此求得所求事件的概率.
解答 解:(1)由题意可知,样本容量n=$\frac{8}{0.02×10}$=40,y=$\frac{2}{40}$×$\frac{1}{10}$=0.005,
x=0.1-(0.02-0.04-0.01-0.005)=0.025.
(2)由题意可知,分数在[80,90)有4人,分别记为a,b,c,d,
分数在[90,100)有2人,分别记为A,B.
从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学有如下种情形:(a,b),(a,c),(a,d),(a,A),(a,B),(b,c),(b,d),(b,A),(b,B),(c,d),(c,A),(c,B),(d,A),(d,B),(A,B),共有15个基本事件;
其中符合所抽取的2名同学中得分在[80,90)内的学生人数的基本事件有:(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)共6个,
所以事件“X=2”的概率为P(X=2)=$\frac{6}{15}$=$\frac{2}{5}$.
点评 本题主要考查等可能事件的概率,频率分布直方图的应用,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
16.若单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$,向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$$+λ\overrightarrow{{e}_{2}}$(λ∈R),且|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{2}$,则λ=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$-1 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
4.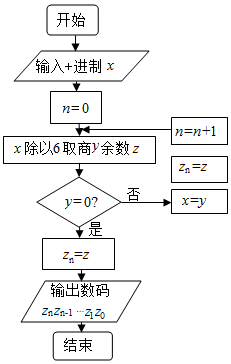 老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
 老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )| A. | 682 | B. | 683 | C. | 692 | D. | 693 |
11.设函数$f(x)=\left\{\begin{array}{l}x,0≤x<1\\ \frac{1}{{f({x+1})}}-1,-1<x<0\end{array}\right.$,g(x)=f(x)-4mx-m,其中m≠0.若函数g(x)在区间(-1,1)上有且仅有一个零点,则实数m的取值范围是( )
| A. | $m≥\frac{1}{4}$或m=-1 | B. | $m≥\frac{1}{4}$ | C. | $m≥\frac{1}{5}$或m=-1 | D. | $m≥\frac{1}{5}$ |
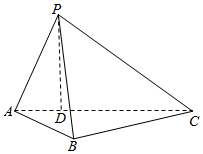 如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.
如图所示,在三棱锥P-ABC中,$AB=BC=2\sqrt{3}$,平面PAC⊥平面ABC,PD⊥AC于点D,AD=2,CD=4,PD=3.