题目内容
1.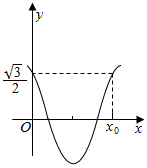 已知函数f(x)=2cos(πx)•cos2$\frac{φ}{2}$-sin(πx)•sinφ-cos(πx)(0≤φ<$\frac{π}{2}$)的部分图象如图所示,则图中的x0的值为( )
已知函数f(x)=2cos(πx)•cos2$\frac{φ}{2}$-sin(πx)•sinφ-cos(πx)(0≤φ<$\frac{π}{2}$)的部分图象如图所示,则图中的x0的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{5}{4}$ | C. | $\frac{5}{2}$ | D. | $\frac{5}{3}$ |
分析 利用已知及三角函数恒等变换的应用化简可得f(x)=cos(πx+φ),又图象过点(0,$\frac{\sqrt{3}}{2}$),结合范围0≤φ<$\frac{π}{2}$,可得:φ=$\frac{π}{6}$,由图象可得:πx0+$\frac{π}{6}$=2-$\frac{π}{6}$,即可解得x0的值.
解答 解:∵f(x)=2cos(πx)•cos2$\frac{φ}{2}$-sin(πx)•sinφ-cos(πx)
=cos(πx)•(1+cosφ)-sin(πx)•sinφ-cos(πx)
=cos(πx)•cosφ-sin(πx)•sinφ
=cos(πx+φ),
又由函数图象可知,图象过点(0,$\frac{\sqrt{3}}{2}$),
∴$\frac{\sqrt{3}}{2}$=cosφ,
∴结合范围0≤φ<$\frac{π}{2}$,可得:φ=$\frac{π}{6}$,
∴由图象可得:cos(πx0+$\frac{π}{6}$)=$\frac{\sqrt{3}}{2}$,可得:πx0+$\frac{π}{6}$=2-$\frac{π}{6}$,解得:x0=$\frac{5}{3}$.
故选:D.
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的图象和性质,由y=Asin(ωx+φ)的部分图象确定其解析式,考查了计算能力和数形结合思想的应用,其中求φ的值是解题的关键,属于中档题.

练习册系列答案
相关题目
15.若直线ax+2y-1=0与直线2x+y-1=0垂直,则a的值是( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
16.若单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$,向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$$+λ\overrightarrow{{e}_{2}}$(λ∈R),且|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{2}$,则λ=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$-1 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
6.下列各函数中,图象经过点($\frac{π}{2}$,-1)的是( )
| A. | y=sinx | B. | y=cosx | C. | y=-sinx | D. | y=-cosx |
13.设lgx=a,lgy=b,则lg$\frac{x}{{y}^{2}}$等于( )
| A. | a-2b | B. | 2a-b | C. | a+2b | D. | a-b |
4.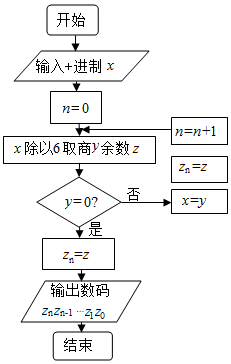 老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
 老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )
老师为哈六中某位同学的高考成绩x设计了一个程序框图,执行如图所示的程序,若输出的数码为3112,则这位同学的高考分数x是( )| A. | 682 | B. | 683 | C. | 692 | D. | 693 |
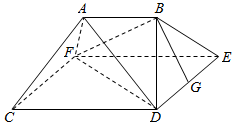 如图,在多面体ABCDEF中,四边形CDEF是正方形,AB∥CD,CD=2AB,G为DE的中点.
如图,在多面体ABCDEF中,四边形CDEF是正方形,AB∥CD,CD=2AB,G为DE的中点.