题目内容
11.写出下面数列的一个通项公式,使它的前4项分别是下列各数:(1)1,-$\frac{1}{2}$,$\frac{1}{3}$,-$\frac{1}{4}$;
(2)2,0,2,0.
分析 (1)每项的符号为(-1)n+1,每项的绝对值为$\frac{1}{n}$.即可得出.
(2)根据1+1=2,1-1=0,即可得出.
解答 解:(1)其符号为(-1)n+1,其每项的绝对值为$\frac{1}{n}$.
∴an=$(-1)^{n+1}\frac{1}{n}$.
(2)an=1+(-1)n+1.
点评 本题考查了通过观察分析猜想归纳得出数列的通项公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
5.在一次导弹实验中,为了确定爆炸点的位置,设立了A、B、C三个观测点.已知B在A的正西方向4a米处,C在A的正南方向a米处,实验中,在B,C两点听到导弹着地时的爆炸声比在A点分别晚2秒和1秒,且声速v=a米/秒,则此导弹爆炸点离A点的 距离为( )
| A. | a米 | B. | 2a米 | C. | 3a米 | D. | 4a米 |
2.在△ABC中,B=$\frac{π}{3}$,AB=2,D为AB中点,△BCD的面积为$\frac{3\sqrt{3}}{4}$,则AC等于( )
| A. | 2 | B. | $\sqrt{7}$ | C. | $\sqrt{10}$ | D. | $\sqrt{19}$ |
6.下列叙述正确的是( )
| A. | 数列1,3,5,7与7,5,3,1是相同的数列 | |
| B. | 数列0,1,2,3,…可以表示为{n} | |
| C. | 数列0,1,0,1,…是常数列 | |
| D. | 数列{$\frac{n}{n+1}$}是递增数列 |
16.若单位向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$的夹角为$\frac{π}{3}$,向量$\overrightarrow{a}$=$\overrightarrow{{e}_{1}}$$+λ\overrightarrow{{e}_{2}}$(λ∈R),且|$\overrightarrow{a}$|=$\frac{\sqrt{3}}{2}$,则λ=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$-1 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
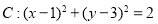 被直线
被直线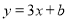 所截得的线段的长度等于2,则
所截得的线段的长度等于2,则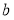 等于( )
等于( )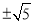 B.
B.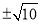 C.
C.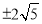 D.
D.