题目内容
已知函数f(x)=ln(1+x)-ln(1-x),x∈(-1,1).判断命题|f(x)|≥2|x|是否正确.
考点:对数函数的图像与性质,对数的运算性质
专题:函数的性质及应用
分析:根据题意,构造函数g(x)=f(x)-2x,利用函数的导数与奇偶性,判断g(x)=f(x)-2x≥0,是否成立,从而判断|f(x)|≥2|x|是否成立.
解答:
解:∵函数f(x)=ln(1+x)-ln(1-x),x∈(-1,1);
∴当x∈[0,1)时,|f(x)|≥2|x|?f(x)-2x≥0,
令g(x)=f(x)-2x=ln(1+x)-ln(1-x)-2x,x∈[0,1);
∵g′(x)=
+
-2=
≥0,
∴g(x)在[0,1)上单调递增,
∴g(x)=f(x)-2x≥g(0)=0,
∴f(x)≥2x;
又∵f(x)与y=2x为奇函数,
∴|f(x)|≥2|x|在x∈(-1,1)上成立,
即|f(x)|≥2|x|是正确的.
∴当x∈[0,1)时,|f(x)|≥2|x|?f(x)-2x≥0,
令g(x)=f(x)-2x=ln(1+x)-ln(1-x)-2x,x∈[0,1);
∵g′(x)=
| 1 |
| 1+x |
| 1 |
| 1-x |
| 2x2 |
| 1-x2 |
∴g(x)在[0,1)上单调递增,
∴g(x)=f(x)-2x≥g(0)=0,
∴f(x)≥2x;
又∵f(x)与y=2x为奇函数,
∴|f(x)|≥2|x|在x∈(-1,1)上成立,
即|f(x)|≥2|x|是正确的.
点评:本题考查了函数的奇偶性与单调性的应用问题,也考查了不等式的应用问题,是综合性题目.

练习册系列答案
相关题目
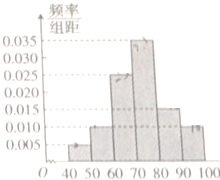 某市从2014届高中毕业生中抽取1000名学生的数学成绩作为样本进行统计,其频率分布直方图如图所示,则这1000名学生的数学平均成绩的最大值可能为( )
某市从2014届高中毕业生中抽取1000名学生的数学成绩作为样本进行统计,其频率分布直方图如图所示,则这1000名学生的数学平均成绩的最大值可能为( )| A、67.50 |
| B、72.50 |
| C、76.50 |
| D、77.50 |