题目内容
15.已知点P为椭圆$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{3}$=1上一点,F1,F2分别为椭圆的左右焦点(1)若|PF1|=4,N为PF1的中点,则ON=2$\sqrt{3}$-2.
(2)若PF1与y轴的交点M恰为PF1的中点,则M的坐标(0,±$\frac{\sqrt{3}}{4}$).
分析 (1)作图分析可得ON是△F1PF2的中位线,从而解得;
(2)作图分析可得,先求点P的坐标,再求点M的坐标.
解答 解:(1)如图,ON是△F1PF2的中位线,
∵|PF1|=4,|PF1|+|PF2|=4$\sqrt{3}$,
∴|PF2|=4$\sqrt{3}$-4,
∴ON=$\frac{1}{2}$(4$\sqrt{3}$-4)=2$\sqrt{3}$-2; ,
,
(2)如图所示, ,
,
由$\frac{9}{12}+\frac{{y}^{2}}{3}$=1解得,P(3,±$\frac{\sqrt{3}}{2}$);
故M(0,±$\frac{\sqrt{3}}{4}$).
故答案为:(1)2$\sqrt{3}$-2,(2)(0,±$\frac{\sqrt{3}}{4}$).
点评 本题考查了学生的作图能力及数形结合的思想应用.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
4.已知F1,F2分别是双曲线Γ;$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点,O为双曲线Γ的对称中心,M,N分别在双曲线Γ的两条渐近线上,∠MF2O=∠MNO=90°,若NF2∥OM,则双曲线r的渐近线方程为( )
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\frac{\sqrt{2}}{2}$x | C. | y=±$\sqrt{2}$x | D. | y=±$\sqrt{3}$x |
6.已知{1,2}⊆M?{1,2,3,4},则这样的集合M有( )个.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.若定义在R上的函数f(x)满足:①x<0时,f(x)=ln(-x);②当x≥0时,f(x+2)=f(x),图象关于x=1对称,③当x∈[0,1]时,f(x)=x,则函数g(x)=f(x)-$\frac{1}{2014}$x的零点有( )
| A. | 1008个 | B. | 2014个 | C. | 2015个 | D. | 4028个 |
10.如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的面积是( ) 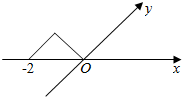

| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
7.设数f(log2x)的定义域是(2,4),则函数$f({\frac{x}{2}})$的定义域是( )
| A. | (2,4) | B. | (2,8) | C. | (8,32) | D. | $(\frac{1}{2},1)$ |
4.在△ABC中,G为△ABC的重心,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{BG}$=( )
| A. | -$\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{2}{3}$$\overrightarrow{b}$ | C. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ |
5.已知抛物线y2=4x上的两点A,B满足|AB|=6,则弦AB中点到y轴的最小距离为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |