题目内容
2.张家的3个鸡仔钻进了李家装有3个鸡仔的鸡笼里,现打开笼门,让鸡仔一个一个地走出来,若第一个走出来的是张家的鸡仔,那么第二个走出的也是张家的鸡仔的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
分析 5只鸡仔中有2个满足条件,从而求出满足条件的概率即可.
解答 解:若第一个走出来的是张家的鸡仔,
则还有2个张家的鸡仔,3个李家的鸡仔,
故走出的是张家的鸡仔的概率p=$\frac{2}{5}$,
故选:A.
点评 此题是个中档题.本题考查的是一个古典概型,解决古典概型问题时先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.同时学生分析问题解决问题的能力.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
13.“p∨q为假命题”是“¬p为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x+1},x≤0}\\{1-lo{g}_{2}x,x>0}\end{array}\right.$则f(f(4))=1.
14.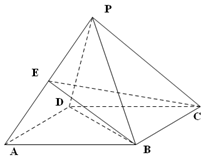 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,
(1)证明:PC∥面EBD;
(2)求三棱锥P-BCE的体积.
 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,E为PA的中点,(1)证明:PC∥面EBD;
(2)求三棱锥P-BCE的体积.
12.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{3}=1(a>0)$的一条渐近线过点$(2,\sqrt{3})$,且双曲线的一个焦点在抛物线y2=2px(p>0)的准线上,则p等于( )
| A. | $\sqrt{7}$ | B. | $2\sqrt{7}$ | C. | 2 | D. | 1 |