题目内容
18.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是40cm3,表面积是32+16$\sqrt{13}$cm2.
分析 由几何体的三视图知该几何体是三棱柱与两个相同的四棱锥的组合体,
画出图形结合图形求出它的体积与表面积.
解答 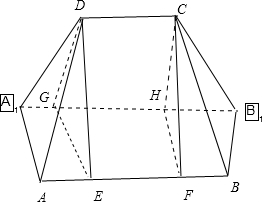 解:由该几何体的三视图,知该几何体是三棱柱与两个相同的四棱锥的组合体,
解:由该几何体的三视图,知该几何体是三棱柱与两个相同的四棱锥的组合体,
如图所示;
该组合体的体积为
V=${V}_{四棱锥D-AE{GA}_{1}}$+V三棱柱DEG-CFH+${V}_{四棱锥C-BF{HD}_{1}}$
=$\frac{1}{3}$×(2×4)×3+($\frac{1}{2}$×4×3)×4+$\frac{1}{3}$×(2×4)×3
=8+24+8
=40(cm3);
它的表面积为
S=${S}_{矩形A{{BB}_{1}A}_{1}}$+2S梯形ABCD+2${S}_{△A{DA}_{1}}$
=8×4+2×$\frac{1}{2}$×(4+8)×$\sqrt{{2}^{2}{+3}^{2}}$+2×$\frac{1}{2}$×4×$\sqrt{{2}^{2}{+3}^{2}}$
=32+16$\sqrt{13}$cm2.
故答案为:40,32+16$\sqrt{13}$.
点评 本题考查利用几何体的三视图求体积与表面积的应用问题,是基础题.

练习册系列答案
相关题目
13.“p∨q为假命题”是“¬p为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x+1},x≤0}\\{1-lo{g}_{2}x,x>0}\end{array}\right.$则f(f(4))=1.
8.已知某程序框图如图所示,则该程序运行后输出的结果为( )


| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |