题目内容
16.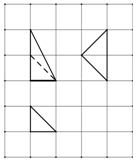 某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )
某几何体的三视图如图所示,网格纸的小方格是边长为1的正方形,则该几何体中最长的棱长是( )| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $\sqrt{7}$ | D. | 3 |
分析 几何体为三棱锥,作出几何体的直观图,根据三视图和勾股定理计算边长即可得出答案.
解答 解:由三视图可知几何体为三棱锥C-ABD,直观图如图所示:
由三视图可知BC⊥平面ABD,△ABD为都腰三角形,AB=2,AD=BD=$\sqrt{2}$,BC=1,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{5}$,CD=$\sqrt{B{D}^{2}+B{C}^{2}}$=$\sqrt{3}$,
∴几何体的最长的棱长为$\sqrt{5}$.
故选:A.
点评 本题考查了棱锥的三视图,属于基础题.

练习册系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x+1},x≤0}\\{1-lo{g}_{2}x,x>0}\end{array}\right.$则f(f(4))=1.
4.如图是用函数拟合解决实际问题的流程图,则矩形框中依次应填入( )
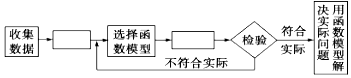

| A. | 整理数据、求函数关系式 | B. | 画散点图、进行模型修改 | ||
| C. | 画散点图、求函数关系式 | D. | 整理数据、进行模型修改 |
8.已知某程序框图如图所示,则该程序运行后输出的结果为( )


| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
 某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.
某少数民族的刺绣有着悠久的历史,如图①②③④是刺绣中最简单的四个图案,这些图案都是由小正方形构成的,小正方形的个数越多刺绣越漂亮.现按同样的规律刺绣,设第n个图案包含f(n)个小正方形.