题目内容
15．若复数z=$\frac{3+i}{1+2i}$，则|z|=（ ）| A． | $\frac{\sqrt{2}}{5}$ | B． | 2$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
分析 化简复数z，求出它的模长即可．
解答 解：z=$\frac{3+i}{1+2i}$=$\frac{（3+i）（1-2i）}{（1+2i）（1-2i）}$=$\frac{5-5i}{5}$1-i，
∴|z|=$\sqrt{{1}^{2}+（-1）^{2}}$=$\sqrt{2}$，
故选：C
点评 本题考查了复数的化简与模长的计算问题，是基础题目．
练习册系列答案
相关题目
20．已知命题p：“1，b，4”成等比数列”，命题q：“b=2”，那么p成立是q成立的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
7．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x+1}，x≤0}\\{1-lo{g}_{2}x，x＞0}\end{array}\right.$则f（f（4））=1．
4．如图是用函数拟合解决实际问题的流程图，则矩形框中依次应填入（ ）
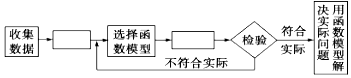
| A． | 整理数据、求函数关系式 | B． | 画散点图、进行模型修改 | ||
| C． | 画散点图、求函数关系式 | D． | 整理数据、进行模型修改 |
某少数民族的刺绣有着悠久的历史，如图①②③④是刺绣中最简单的四个图案，这些图案都是由小正方形构成的，小正方形的个数越多刺绣越漂亮．现按同样的规律刺绣，设第n个图案包含f（n）个小正方形．