题目内容
1.设f(x)定义如下面数表,{xn}满足x0=5,且对任意自然数n均有xn+1=f(xn),则x2015的值为( )| x | 1 | 2 | 3 | 4 | 5 |
| f(x) | 4 | 1 | 3 | 5 | 2 |
| A. | 1 | B. | 2 | C. | 5 | D. | 4 |
分析 由已知结合图表依次求出前几项,得到周期,由周期性得答案.
解答 解:由x0=5,且xn+1=f(xn),可得:
x1=f(x0)=f(5)=2,x2=f(x1)=f(2)=1,
x3=f(x2)=f(1)=4,x4=f(x3)=f(4)=5,
x5=f(x4)=f(5)=2,…
由上可知,xn以4为周期出现,则x2015=x4×503+3=x3=4.
故选:D.
点评 本题考查函数值的求法,考查学生读取图表的能力,关键是对题意的理解,是基础的计算题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11. 已知函数f(x)=|x-1|+|x-2|.
已知函数f(x)=|x-1|+|x-2|.
(1)用分段函数的形式表示该函数,并在所给的坐标系中画出该函数的图象;
(2)写出该函数的值域、单调区间(不要求证明);
(3)求不等式f(x)≤3的解集.
 已知函数f(x)=|x-1|+|x-2|.
已知函数f(x)=|x-1|+|x-2|.(1)用分段函数的形式表示该函数,并在所给的坐标系中画出该函数的图象;
(2)写出该函数的值域、单调区间(不要求证明);
(3)求不等式f(x)≤3的解集.
10.下列算法框中表示处理框的是( )
| A. | 菱形框 | B. | 平行四边形框 | C. | 矩形框 | D. | 三角形框 |
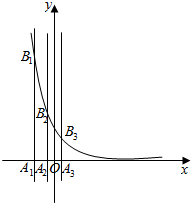 (文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.