题目内容
6.已知f(x)=x2-2x,g(x)=ax+2(a>0),若命题:对于任意的x1∈[-1,2],存在x2∈[-1,2],使f(x1)=g(x2)为真命题,求a的范围.分析 根据条件求出f(x)和g(x)的最值,建立不等式关系即可.
解答 解:f(x)=x2-2x的对称轴为x=1,
当x∈[-1,2],当x=1时,函数取得最小值f(1)=1-2=-1,
当x=-1时,函数取得最大f(-1)=1+2=3,
则-1≤f(x)≤3,即f(x)的值域为[-1,3],
当x∈[-1,2]时,g(x)=ax+2为增函数,
则g(-1)≤g(x)≤g(2),
即2-a≤g(x)≤2a+2,即g(x)的值域为[2-a,2+2a],
若对于任意的x1∈[-1,2],存在x2∈[-1,2],使f(x1)=g(x2),
则$\left\{\begin{array}{l}{2a+2≥3}\\{2-a≤-1}\end{array}\right.$,即$\left\{\begin{array}{l}{a≥1}\\{a≥3}\end{array}\right.$,解得a≥3.
点评 本题主要考查函数最值的应用,根据条件求出函数的最值,结合函数最值的关系建立不等式是解决本题的关键.

练习册系列答案
相关题目
16.五名男同学,三名女同学外出春游,平均分成两组,每组4人,则女同学不都在同一组的不同分法有( )
| A. | 30种 | B. | 65种 | C. | 35种 | D. | 70种 |
11.设$a={log_{\frac{1}{2}}}3,b={(\frac{1}{2})^{0.4}},c={3^{\frac{1}{2}}}$则a,b,c的大小关系是( )
| A. | c>b>a | B. | c>a>b | C. | b>a>c | D. | a>b>c |
15.已知圆:(x-2)2+y2=3与双曲线:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1,(a>0,b>0)$的渐近线相切,则双曲线的离心率为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 4 |
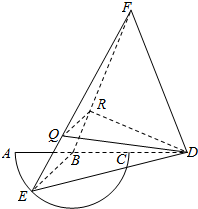 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.