题目内容
16.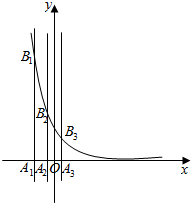 (文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.
(文)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数f(x)=($\frac{1}{2}$)x的图象分别交于点An与Bn(如图所示),记Bn的坐标为(an,bn),直角梯形A1A2B2B1、A2A3B3B2的面积分别为s1和s2,一般地记直角梯形AnAn+1Bn+1Bn的面积为sn.(1)求证:数列{sn}是公比绝对值小于1的等比数列;
(2)设数列{an}的首项为p=-1,公差d=1,是否存在这样的正整数n,构成以bn,bn+1,bn+2为边长的三角形?并请说明理由;
(3))设{an}的公差d=1,是否存在这样的实数p使得(1)中无穷等比数列{sn}各项的和S>2010?如果存在,给出一个符合条件的p值;如果不存在,请说明理由.
分析 (1)求出{an}的通项公式,带入f(x)得出{bn}的通项公式,带入梯形面积公式得出{sn}的通项公式,证明$\frac{{s}_{n+1}}{{s}_{n}}$为绝对值小于1的常数;
(2)求出{bn}的通项公式,采用假设法推导结论或矛盾;
(3)求出{sn}的通项公式,得出S,采用假设法推导结论或矛盾.
解答 解:(1)an=p+(n-1)d,bn=f(an)=($\frac{1}{2}$)p+(n-1)d,
∴sn=$\frac{1}{2}$(bn+bn+1)d=$\frac{1}{2}$[($\frac{1}{2}$)p+(n-1)d+($\frac{1}{2}$)p+nd]d=$\frac{1}{2}$•($\frac{1}{2}$)p+nd•[($\frac{1}{2}$)-d+1]•d.
∴$\frac{{s}_{n+1}}{{s}_{n}}$=$\frac{(\frac{1}{2})^{p+(n+1)d}}{(\frac{1}{2})^{p+nd}}$=($\frac{1}{2}$)d,∵d>0,∴0<($\frac{1}{2}$)d<1,
∴数列{sn}是公比绝对值小于1的等比数列.
(2)an=-1+(n-1)×1=n-2.bn=($\frac{1}{2}$)n-2=2•($\frac{1}{2}$)n-1,
∴{bn}是以2位首项,以$\frac{1}{2}$为公比的等比数列,
∴bn>bn+1>bn+2.
假设存在正整数n,构成以bn,bn+1,bn+2为边长的三角形,
则bn+1+bn+2>bn,即($\frac{1}{2}$)n-1+($\frac{1}{2}$)n-($\frac{1}{2}$)n-2>0,
($\frac{1}{2}$)n-2($\frac{1}{2}$+$\frac{1}{4}$-1)>0,∴(-$\frac{1}{4}$)×($\frac{1}{2}$)n-2>0.显然不成立.
∴不存在正整数n,构成以bn,bn+1,bn+2为边长的三角形.
(3)设{sn}的公比为q,则s1=3×($\frac{1}{2}$)p+2,q=$\frac{1}{2}$.∴S=$\frac{{s}_{1}}{1-q}$=$\frac{3}{{2}^{p+1}}$.
假设存在实数p使得无穷等比数列{sn}各项的和S>2010,
则$\frac{3}{{2}^{p+1}}$>2010,即2p<$\frac{3}{4020}$=$\frac{1}{1340}$,
∴p<-log21340<-10.
∴存在p=-11使得无穷等比数列{sn}各项的和S>2010.
点评 本题考查了数列的通项公式,数列求和及数列应用,采用假设法解决存在性问题是重要的一种方法.

 名校课堂系列答案
名校课堂系列答案| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$+1 |
