题目内容
11. 已知函数f(x)=|x-1|+|x-2|.
已知函数f(x)=|x-1|+|x-2|.(1)用分段函数的形式表示该函数,并在所给的坐标系中画出该函数的图象;
(2)写出该函数的值域、单调区间(不要求证明);
(3)求不等式f(x)≤3的解集.
分析 (1)分三段讨论并根据表达式画出函数图象;
(2)由图象得出函数的单调区间和值域;
(3)分三段讨论得出不等式的解集.
解答 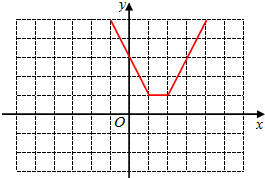 解:(1)f(x)=|x-1|+|x-2|,分三段讨论如下:
解:(1)f(x)=|x-1|+|x-2|,分三段讨论如下:
①当x≥2时,f(x)=2x-3;
②当1≤x<2时,f(x)=1;
③当x<1时,f(x)=-2x+3,
所以,f(x)=$\left\{\begin{array}{l}{2x-3,x≥2}\\{1,1≤x<2}\\{-2x+3,x<1}\end{array}\right.$,图象如右图;
(2)函数f(x)的值域为:[1,+∞),
函数f(x)的单调增区间为:[2,+∞),
函数f(x)的单调减区间为:(-∞,1];
(3)要解不等式f(x)≤3,需分三段讨论如下:
①当x≥2时,f(x)=2x-3≤3,解得,2≤x≤3;
②当1≤x<2时,f(x)=1≤3恒成立,所以,1≤x<2;
③当x<1时,f(x)=-2x+3≤3,解得,0≤x<1,
综合以上讨论得,f(x)≤3的解集为:[0,3].
点评 本题主要考查了分段函数的图象和性质,涉及分段函数的表示,图象的作法,值域,单调区间和不等式的解法,属于中档题.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
12.已知圆C1:x2+y2-$\frac{2}{\sqrt{a}}$x+$\frac{1}{a}$-$\frac{9}{4}$=0,C2:x2+y2-$\frac{2}{\sqrt{b}}$y+$\frac{1}{b}$-$\frac{1}{4}$=0,其中a>0,b>0,a+b=1,则两圆公切线有多少条( )
| A. | 1条或者3条 | B. | 1条或者2条 | C. | 2条或者3条 | D. | 4条或者3条 |
6.己知A、F分别为双曲线C的左顶点和右焦点,点D在C上,△AFD是等腰直角三角形,且∠AFD=90°,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$+1 |
16.五名男同学,三名女同学外出春游,平均分成两组,每组4人,则女同学不都在同一组的不同分法有( )
| A. | 30种 | B. | 65种 | C. | 35种 | D. | 70种 |