题目内容
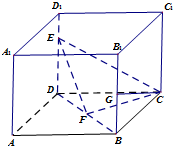 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱DD1上的动点,F,G分别是BD,BB1的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱DD1上的动点,F,G分别是BD,BB1的中点.(1)求证:EF⊥CF.
(2)当点E是棱DD1上的中点时,求异面直线EF与CG所成角的余弦值.
(3)当二面角E-CF-D达到最大时,求其余弦值.
考点:与二面角有关的立体几何综合题,异面直线及其所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)利用线面垂直的判定定理,证明CF⊥面BB1D1D,即可证明EF⊥CF.
(2)连接A1E,AF.证明∠A1EF或其补角为异面直线EF与CG所成角,求出△A1EF的三边,利用余弦定理,可求异面直线EF与CG所成角的余弦值.
(3)确定∠EFD为二面角E-CF-D的平面角,当E与D1重合时,二面角E-CF-D达到最大,利用余弦定理求其余弦值.
(2)连接A1E,AF.证明∠A1EF或其补角为异面直线EF与CG所成角,求出△A1EF的三边,利用余弦定理,可求异面直线EF与CG所成角的余弦值.
(3)确定∠EFD为二面角E-CF-D的平面角,当E与D1重合时,二面角E-CF-D达到最大,利用余弦定理求其余弦值.
解答:
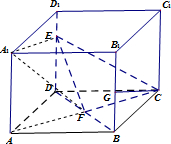 (1)证明:∵F为BD的中点,∴CF⊥BD…(1分)
(1)证明:∵F为BD的中点,∴CF⊥BD…(1分)
又∵DD1⊥面ABCD,∴DD1⊥CF…(2分)
∵DD1∩BD=D,
∴CF⊥面BB1D1D…(3分)
∵EF?面BB1D1D,∴CF⊥EF…(4分);
(2)解:连接A1E,AF.
当点E是棱DD1上的中点时,因为G为BB1的中点,由正方体的性质知A1E∥CG,
故∠A1EF或其补角为异面直线EF与CG所成角.…(5分)
在Rt△DEF中,EF=
=
=
…(6分)
在Rt△A1D1E中,A1E=
=
…(7分)
在Rt△A1AF中,A1F=
=
…(8分)
故在△A1EF中,cos∠A1EF=
=
=
,
∴异面直线EF与CG所成角的余弦值为
…(9分);
(3)解:∵CF⊥面BB1D1D,
∴CF⊥EF,CF⊥DF…(10分)
故∠EFD为二面角E-CF-D的平面角,…(11分)
当E与D1重合时,二面角E-CF-D达到最大.…(12分)
此时,DF=
,DD1=1,EF=
…(13分)
∴cos∠EFD=
=
=
,即当二面角E-CF-D达到最大时其余弦值为
…(14分).
 (1)证明:∵F为BD的中点,∴CF⊥BD…(1分)
(1)证明:∵F为BD的中点,∴CF⊥BD…(1分)又∵DD1⊥面ABCD,∴DD1⊥CF…(2分)
∵DD1∩BD=D,
∴CF⊥面BB1D1D…(3分)
∵EF?面BB1D1D,∴CF⊥EF…(4分);
(2)解:连接A1E,AF.
当点E是棱DD1上的中点时,因为G为BB1的中点,由正方体的性质知A1E∥CG,
故∠A1EF或其补角为异面直线EF与CG所成角.…(5分)
在Rt△DEF中,EF=
(
|
|
| ||
| 2 |
在Rt△A1D1E中,A1E=
1+(
|
| ||
| 2 |
在Rt△A1AF中,A1F=
1+(
|
| ||
| 2 |
故在△A1EF中,cos∠A1EF=
| A1E2+EF2-A1F2 |
| 2A1E•EF |
| ||||||||
2•
|
| ||
| 15 |
∴异面直线EF与CG所成角的余弦值为
| ||
| 15 |
(3)解:∵CF⊥面BB1D1D,
∴CF⊥EF,CF⊥DF…(10分)
故∠EFD为二面角E-CF-D的平面角,…(11分)
当E与D1重合时,二面角E-CF-D达到最大.…(12分)
此时,DF=
| ||
| 2 |
| ||
| 2 |
∴cos∠EFD=
| DF |
| EF |
| ||||
|
| ||
| 3 |
| ||
| 3 |
点评:本题考查线面垂直的判定与性质,考查线线角,面面角,考查余弦定理,考查学生的计算能力,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
阅读如图所示的程序框图,则该算法的功能是( )
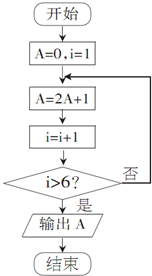

| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前6项的和 |
| C、计算数列{2n-1}前5项的和 |
| D、计算数列{2n-1}前6项的和 |
已知在一个120°的二面角的棱上有两个点A、B,AC、BD分别是在这个二面角的两个半平面内且垂直于AB的线段,又AB=4cm,AC=6cm,BD=8cm,则CD的长为( )
A、2
| ||
B、
| ||
C、2
| ||
D、4
|

 已知△ABC的两顶点坐标A(-1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M.
已知△ABC的两顶点坐标A(-1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M. 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.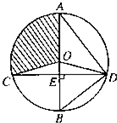 选修4-1几何证明选讲
选修4-1几何证明选讲