题目内容
已知椭圆具有如下性质:若M、N是椭圆C上关于原点对称的两个点,点P是椭圆上的任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,则kPM与kPN之积是与点P位置无关的定值.试写出双曲线
-
=1(a>0,b>0)具有的类似的性质,并加以证明.
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设点M的坐标为(m,n),则点N的坐标为(-m,-n),且
-
=1,又设点P的坐标为(x,y),表示出直线PM和PN的斜率,求得两直线斜率乘积的表达式,把y和x的表达式代入发现结果与p无关.
| m2 |
| a2 |
| n2 |
| b2 |
解答:
解:双曲线的类似的性质为:若M,N是双曲线
-
=1上关于原点对称的两个点,点P是双曲线上的任意一点,当直线PM、PN的斜率都存在,并记为kPM、kPN时,kPM与kPN之积是与点P位置无关的定值.
下面给出证明:
设点M的坐标为(m,n),则点N的坐标为(-m,-n),且
-
=1.
又设点P的坐标为(x,y),由kPM=
,kPN=
得kPM•kPN=
•
=
,①
将y2=
x2-b2,n2=
m2-b2代入①式,得kPM•kPN=
(定值).
| x2 |
| a2 |
| y2 |
| b2 |
下面给出证明:
设点M的坐标为(m,n),则点N的坐标为(-m,-n),且
| m2 |
| a2 |
| n2 |
| b2 |
又设点P的坐标为(x,y),由kPM=
| y-n |
| x-m |
| y+n |
| x+m |
| y-n |
| x-m |
| y+n |
| x+m |
| y2-n2 |
| x2-m2 |
将y2=
| b2 |
| a2 |
| b2 |
| a2 |
| b2 |
| a2 |
点评:本题主要考查了双曲线的性质,考查了学生综合分析问题和解决问题的能力,正确计算是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
双曲线
-y2=1的焦点到渐近线的距离为( )
| x2 |
| 4 |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、3 |
函数y=ln(x+1)与y=
的图象交点的横坐标所在区间为( )
| 1 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
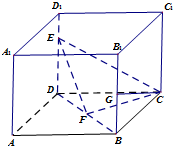 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱DD1上的动点,F,G分别是BD,BB1的中点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱DD1上的动点,F,G分别是BD,BB1的中点.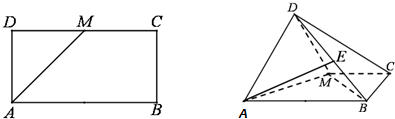
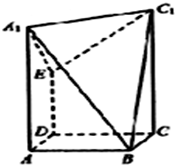 在长方体中ABCD-A1B1C1D1,AB=BC=2,点E是棱DD1的中点,过A1、C1、B三点的平面截去长方体的一个角,又过A1、C1、E三点的平面再截去长方体的另一个角得到如图所示的几何体ABCD-A1C1E
在长方体中ABCD-A1B1C1D1,AB=BC=2,点E是棱DD1的中点,过A1、C1、B三点的平面截去长方体的一个角,又过A1、C1、E三点的平面再截去长方体的另一个角得到如图所示的几何体ABCD-A1C1E