题目内容
2.将函数f(x)=cos2x的图象向右平移$\frac{π}{3}$个单位得到g(x)的图象,若g(x)在(-2m,-$\frac{π}{6}$)和(3m,$\frac{5π}{6}$)上都单调递减,则实数m的取值范围为( )| A. | [$\frac{π}{9}$,$\frac{5π}{18}$) | B. | [$\frac{π}{9}$,$\frac{π}{3}$) | C. | ($\frac{π}{12}$,$\frac{5π}{18}$) | D. | [$\frac{π}{18}$,$\frac{5π}{12}$] |
分析 由函数的图象平移求得函数g(x)的解析式,进一步求出函数(x)的单调减区间,结合函数g(x)在(-2m,-$\frac{π}{6}$)和(3m,$\frac{5π}{6}$)上都单调递减列关于m的不等式组求解.
解答 解:将函数f(x)=2cos2x的图象向右平移$\frac{π}{3}$个单位后得到函数g(x)的图象,
得g(x)=2cos2(x-$\frac{π}{3}$)=2cos(2x-$\frac{2}{3}$π),
由2kπ≤2x-$\frac{2π}{3}$≤2kπ+π,得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$.
若g(x)在(-2m,-$\frac{π}{6}$)上单调递减,则有$\left\{\begin{array}{l}{-\frac{π}{6}≤kπ+\frac{5}{6}π}\\{-2m≥kπ+\frac{π}{3}}\\{-2m<-\frac{π}{6}}\end{array}\right.$,此时k=2,解得$\frac{π}{12}$<m≤$\frac{π}{3}$
若g(x)在(3m,$\frac{5π}{6}$)上单调递减,则有,$\left\{\begin{array}{l}{\frac{5π}{6}≤kπ+\frac{5}{6}π}\\{3m≥kπ+\frac{π}{3}}\\{3m<-\frac{5π}{6}}\end{array}\right.$,此时k=0,解得$\frac{π}{9}$≤m<$\frac{5π}{18}$,
同时成立,取交集,有$\frac{π}{9}$≤m<$\frac{5π}{18}$.
故选:A.
点评 本题考查三角函数的图象变换,考查了y=Asin(ωx+φ)型函数的性质,是中档题.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案| A. | -8 | B. | -6 | C. | 0 | D. | 2 |
| x | 1 | 2 | 3 | 4 | 5 |
| y | 13.2 | m | 14.2 | 15.4 | 16.4 |
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{7}{9}$ | C. | $\frac{4}{5}$ | D. | $\sqrt{13}$ |
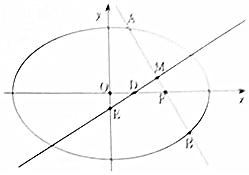 过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.
过椭圆C:$\frac{{x}^{2}}{2}$+y2=1的右焦点F的直线l交椭圆于A,B两点,M是AB的中点.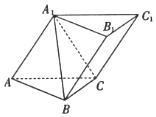 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1⊥底面ABC,△A1AC为等边三角形,AC⊥A1B.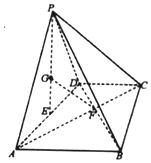 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为梯形,AB∥CD,AB=2DC=2$\sqrt{3}$,且△PAD与△ABD均为正三角形,E为AD的中点,G为△PAD的重心,AC∩BD=F