题目内容

已知菱形ABCD的边长为a，∠DAB=60°，
EC
=2
DE
，则
AE
•
DB
的值为
 
．
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用菱形的性质、向量的三角形法则及其平行四边形法则、数量积运算、向量共线定理即可得出．
解答： 解：如图所示，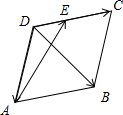
∵
EC
=2
DE
，∴
DE
=
1
3
DC
．
∵菱形ABCD的边长为a，∠DAB=60°，
∴|
DA
|=|
DC
|=a，
DA
•
DC
=|
DA
| |
DC
|cos120°=-
1
2
a2．
DB
=
DA
+
DC
．
∴
AE
•
DB
=(
AD
+
DE
)•(
DA
+
DC
)
=(
AD
+
1
3
DC
)•(
DA
+
DC
)
=-
DA
2+
1
3
DC
2-
2
3
DA
•
DC

=-a2+
1
3
a2+
1
3
a2
=-
1
3
a2．
故答案为：-
1
3
a2．
点评：本题考查了菱形的性质、向量的三角形法则及其平行四边形法则、数量积运算、向量共线定理等基础知识与基本技能方法，考查了推理能力，属于中档题．
练习册系列答案
相关题目
已知偶函数f（x）=ax2+bx+c在点（1，1）处的切线与直线x+2y+9=0垂直，函数g（x）=f（x）+mln（x+1）（m≠0）
（1）求函数f（x）的解析式
（2）当m＜
1
2
时，求函数g（x）的单调区间和极值点．
sin34°sin26°-cos34°cos26°的值为
 
．
对于函数y=f（x），若存在定义域D内某个区间[a，b]，使得y=f（x）在[a，b]上的值域也为[a，b]，则称函数y=f（x）在定义域D上封闭，如果函数f（x）=-
4x
1+|x|
在R上封闭，则b-a=
 
．
已知|
a
|=2，|
b
|=2
2
，|
c
|=2
3
，且
a
+
b
+
c
=
0
，则
a
•
b
+
b
•
c
+
a
•
c
=
 
．
若f（x）=sin（2x+
π
6
）-cos2x，则f（x）在[0，
π
2
]上的最大值与最小值之和为
 
．
已知α，β表示两个不同的平面，m是一条直线，且m?α，则“α∥β”是“m∥β”的
 
条件（填：充分条件、必要条件、充要条件、既不充分也不必要条件）
在（
x
+
1
3x
）5的展开式中的常数项为p，则
∫
1
0
（3x2+p）dx=
 
．
某长方体的所有顶点都在球O的球面上，在球O内任取一点Q，记点Q落入长方体内的概率为P．若球O的半径为1，长方体的长、宽、高分别为x，y，1，则P的最大值为（　　）
A、
3
4π
B、
3
8π
C、
9
4π
D、
9
8π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网