题目内容
12.在等比数列{an}中,若a5+a6+a7+a8=$\frac{15}{8}$,a6a7=-$\frac{9}{8}$,则$\frac{1}{{a}_{5}}$+$\frac{1}{{a}_{6}}$+$\frac{1}{{a}_{7}}$+$\frac{1}{{a}_{8}}$=-$\frac{5}{3}$.分析 由等比数列的性质可得a5a8=a6a7=-$\frac{9}{8}$,由分式的性质化简可得原式=$\frac{{a}_{5}+{a}_{6}+{a}_{7}+{a}_{8}}{{a}_{6}{a}_{7}}$代入数据化简可得.
解答 解:由等比数列的性质可得a5a8=a6a7=-$\frac{9}{8}$,
∴$\frac{1}{{a}_{5}}$+$\frac{1}{{a}_{6}}$+$\frac{1}{{a}_{7}}$+$\frac{1}{{a}_{8}}$=($\frac{1}{{a}_{5}}$+$\frac{1}{{a}_{8}}$)+($\frac{1}{{a}_{6}}$+$\frac{1}{{a}_{7}}$)=$\frac{{a}_{5}+{a}_{8}}{{a}_{5}{a}_{8}}$+$\frac{{a}_{6}+{a}_{7}}{{a}_{6}{a}_{7}}$=$\frac{{a}_{5}+{a}_{6}+{a}_{7}+{a}_{8}}{{a}_{6}{a}_{7}}$=$\frac{\frac{15}{8}}{-\frac{9}{8}}$=-$\frac{5}{3}$,
故答案为:-$\frac{5}{3}$
点评 本题考查等比数列的前n项和和性质,涉及分式的运算性质,属中档题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
10.若函数f(x)=$\frac{|x-1|}{x+2}$与g(x)=k(x-1)3的图象恰好有两个公共点,则实数k的取值范围是( )
| A. | (-∞,-$\frac{1}{4}$) | B. | (0,+∞) | C. | (-∞,-$\frac{1}{4}$)∪(0,+∞) | D. | (-$\frac{1}{4}$,0) |
1.执行如图的程序框图,如果输入的x的值为1,则输出的x的值为( )


| A. | 4 | B. | 13 | C. | 40 | D. | 121 |
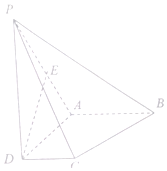 如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.
如图,四棱锥P-ABCD中,底面ABCD是梯形,∠ADC=∠BAD=90°且AB=AD=PD=2CD=2,PD⊥平面ABCD,E是PA中点.