��Ŀ����
7����ԲC1��x2+y2=4��ÿһ��������걣�ֲ��䣬�������Ϊԭ����$\sqrt{5}$���õ�����C2����1��д��C2�IJ������̣�
��2����֪F��-4��0����ֱ��l�IJ�������Ϊ$\begin{array}{l}\left\{\begin{array}{l}x=-4+\sqrt{2}t\\ y=\sqrt{2}t\end{array}\right.\end{array}$��tΪ��������ֱ��l������C2��A��B���㣬��|AF|+|BF|
���� ��1���������C2����ͨ���̣�����д��C2�IJ������̣�
��2����ֱ�ߵIJ������̱�Ϊ$\left\{\begin{array}{l}{x=-4+\frac{\sqrt{2}}{2}t��}\\{y=\frac{\sqrt{2}}{2}t��}\end{array}\right.$��t��Ϊ����������x2+5y2=20�������$3t{��}^{2}-4\sqrt{2}t��-4=0$�����ò����ļ������壬������|AF|+|BF|��
��� �⣺��1����ԲC1������һ��P��x��y��������C2������һ��P'��x'��y'����
���������$\left\{\begin{array}{l}x'=\sqrt{5}x\\ y'=y\end{array}\right.$����$\left\{\begin{array}{l}x=\frac{1}{{\sqrt{5}}}x'\\ y=y'\end{array}\right.$����C1����x2+y2=4���ɵ�$\frac{{{{x'}^2}}}{20}+\frac{{{{y'}^2}}}{4}=1$��
������C2�IJ�������Ϊ$\left\{\begin{array}{l}x=2\sqrt{5}cos��\\ y=2sin��\end{array}\right.����Ϊ������$
��2����ֱ�ߵIJ������̱�Ϊ$\left\{\begin{array}{l}{x=-4+\frac{\sqrt{2}}{2}t��}\\{y=\frac{\sqrt{2}}{2}t��}\end{array}\right.$��t��Ϊ����������x2+5y2=20��
�����$3t{��}^{2}-4\sqrt{2}t��-4=0$���跽�̵�����ʵ��Ϊt'1��t'2����t'1+t'2=$\frac{4\sqrt{2}}{3}$��t'1t'2=-$\frac{4}{3}$��
��|AF|+|BF|=|t'1-t'2|=$\sqrt{\frac{32}{9}+4��\frac{4}{3}}$=$\frac{4\sqrt{5}}{3}$��
���� ���⿼��������̣���������ļ�����������ã������е��⣮

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�| A�� | a��b��c | B�� | c��b��a | C�� | c��a��b | D�� | b��c��a |
| A�� | 36 | B�� | 60 | C�� | 72 | D�� | 96 |
| ���� | ������ | �ϼ� | |
| �� | 10 | 20 | 30 |
| Ů | 15 | 5 | 20 |
| �ϼ� | 25 | 25 | 50 |
| P��K2��k�� | 0.100 | 0.050 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 6.635 | 10.828 |
| A�� | ��95%�İ�����Ϊ�Ե��ӽ�Ŀ����������Ա��� | |
| B�� | ��99%�İ�����Ϊ�Ե��ӽ�Ŀ����������Ա��� | |
| C�� | ��99%�İ�����Ϊ�Ե��ӽ�Ŀ����������Ա��й� | |
| D�� | ��95%�İ�����Ϊ�Ե��ӽ�Ŀ����������Ա��й� |
| A�� | ��ABC���ڲ� | B�� | ��ABC���ⲿ | C�� | P���߶�AC�� | D�� | P���߶�AB�� |
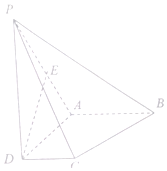 ��ͼ������P-ABCD�У�����ABCD�����Σ���ADC=��BAD=90����AB=AD=PD=2CD=2��PD��ƽ��ABCD��E��PA�е㣮
��ͼ������P-ABCD�У�����ABCD�����Σ���ADC=��BAD=90����AB=AD=PD=2CD=2��PD��ƽ��ABCD��E��PA�е㣮