题目内容
20.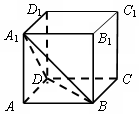 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 由已知可得AC1⊥平面A1DB,可得P为AC1与截面A1DB的垂足时线段AP最小,然后利用等积法求解.
解答 解:如图,连接AC1交截面A1DB于P,由CC1⊥底面,可得CC1⊥BD,又AC⊥BD,可得BD⊥平面ACC1,则AC1⊥BD.
同理可得AC1⊥A1B,得到AC1⊥平面A1DB,此时线段AP最小.
由棱长为1,可得等边三角形A1DB的边长为$\sqrt{2}$,∴${S}_{△{A}_{1}BD}=\frac{1}{2}×\sqrt{2}×\frac{\sqrt{6}}{2}=\frac{\sqrt{3}}{2}$.
由${V}_{{A}_{1}-ABD}={V}_{A-{A}_{1}BD}$,可得$\frac{1}{3}×\frac{1}{2}×1×1×1=\frac{1}{3}×\frac{\sqrt{3}}{2}AP$,得AP=$\frac{\sqrt{3}}{3}$.
故选:C.
点评 本题考查点、线、面间的距离的求法,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
5.设{an}是首项为a1,公差为-2的等差数列,Sn为前n项和,若S1,S2,S4成等比数列,则a1=( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
19.函数y=x$\sqrt{1-{x^2}}$是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 即是奇函数又是偶函数 | D. | 非奇非偶函数 |
 如图,椭圆x2+$\frac{y^2}{4}$=1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距
如图,椭圆x2+$\frac{y^2}{4}$=1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距