题目内容
19.函数y=x$\sqrt{1-{x^2}}$是( )| A. | 奇函数 | B. | 偶函数 | ||
| C. | 即是奇函数又是偶函数 | D. | 非奇非偶函数 |
分析 可先求出该函数定义域为[-1,1],关于原点对称,又可求得$(-x)\sqrt{1-(-x)^{2}}=-x\sqrt{1-{x}^{2}}$,从而可判断出该函数为奇函数.
解答 解:解1-x2≥0得,-1≤x≤1;
又$-x\sqrt{1-(-x)^{2}}=-x\sqrt{1-{x}^{2}}$;
∴函数$y=x\sqrt{1-{x}^{2}}$为奇函数.
故选:A.
点评 考查一元二次不等式的解法,以及奇函数的定义及判断方法.

练习册系列答案
相关题目
20.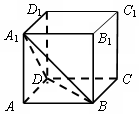 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
10.在△ABC中,A:B:C=4:1:1,则a:b:c=( )
| A. | 4:1:1 | B. | 2:1:1 | C. | 3:1:1 | D. | $\sqrt{3}$:1:1 |
7.已知A(2,4)关于直线x-y+1=0对称的点为B,则B满足的直线方程为( )
| A. | x+y=0 | B. | x-y+2=0 | C. | x+y-5=0 | D. | x-y=0 |
4.设数列{an},{bn}都是等差数列,且a1=12,b1=48,a2+b2=60,则由an+bn所组成的数列的第99项的值为( )
| A. | .60 | B. | 70 | C. | 99 | D. | 100 |
11.已知x,y之间的一组数据如下表:
对于表中数据则根据最小二乘法的思想得拟合程度最好的直线是( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 3 | 4 | 6 | 8 | 9 |
| A. | y=x+1 | B. | y=2x-1 | C. | y=$\frac{8}{5}$x-$\frac{2}{5}$ | D. | y=$\frac{3}{2}$x |
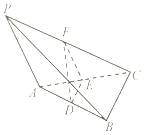 已知,如图,P是平面ABC外一点,PA不垂直于平面ABC,E,F分别是线段AC,PC的中点,D是线段AB上一点,AB=AC,PB=PC,DE⊥EF.
已知,如图,P是平面ABC外一点,PA不垂直于平面ABC,E,F分别是线段AC,PC的中点,D是线段AB上一点,AB=AC,PB=PC,DE⊥EF.