题目内容
12.函数$f(x)=\frac{{{{(x+3)}^0}}}{{\sqrt{|x|-x}}}$的定义域是(-∞,-3)∪(-3,0).分析 由0指数幂的底数不为0,分母中根式内部的代数式大于等于0联立不等式组求解.
解答 解:由$\left\{\begin{array}{l}{x+3≠0}\\{|x|-x>0}\end{array}\right.$,解得x<0且x≠-3.
∴函数$f(x)=\frac{{{{(x+3)}^0}}}{{\sqrt{|x|-x}}}$的定义域是:(-∞,-3)∪(-3,0).
故答案为:(-∞,-3)∪(-3,0).
点评 本题考查函数的定义域及其求法,是基础的计算题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
20.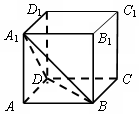 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
10.在△ABC中,A:B:C=4:1:1,则a:b:c=( )
| A. | 4:1:1 | B. | 2:1:1 | C. | 3:1:1 | D. | $\sqrt{3}$:1:1 |
11.已知x,y之间的一组数据如下表:
对于表中数据则根据最小二乘法的思想得拟合程度最好的直线是( )
| x | 2 | 3 | 4 | 5 | 6 |
| y | 3 | 4 | 6 | 8 | 9 |
| A. | y=x+1 | B. | y=2x-1 | C. | y=$\frac{8}{5}$x-$\frac{2}{5}$ | D. | y=$\frac{3}{2}$x |
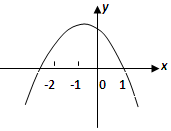 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0