题目内容
15. 如图,椭圆x2+$\frac{y^2}{4}$=1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距
如图,椭圆x2+$\frac{y^2}{4}$=1的左、右顶点分别为A、B,双曲线Γ以A、B为顶点,焦距为2$\sqrt{5}$,点P是Γ上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为k,O为坐标原点.
(1)求双曲线Γ的方程;
(2)求点M的纵坐标yM的取值范围;
(3)是否存在定直线l,使得直线BP与直线OM关于直线l对称?若存在,求直线l方程,若不存在,请说明理由.
分析 (1)求由题意,a=1,c=$\sqrt{5}$,b=2,即可双曲线Γ的方程;
(2)yM=$\frac{4k}{4+{k}^{2}}$=$\frac{4}{k+\frac{4}{k}}$在(0,2)上单调递增,即可求点M的纵坐标yM的取值范围;
(3)求出kOM+kBP=0,可得直线BP与OM关于直线x=$\frac{1}{2}$对称
解答 解:(1)由题意,a=1,c=$\sqrt{5}$,b=2,
∴双曲线Γ的方程${x}^{2}-\frac{{y}^{2}}{4}$=1;
(2)由题意,设P(x1,y1),Q(x2,y2),
直线AP的方程y=k(x+1)(0<k<2),代入椭圆方程,整理得(4+k2)x2+2k2x+k2-4=0
∴x=-1或x2=$\frac{4-{k}^{2}}{4+{k}^{2}}$,
∴Q($\frac{4-{k}^{2}}{4+{k}^{2}}$,$\frac{8k}{4+{k}^{2}}$),M(-$\frac{{k}^{2}}{4+{k}^{2}}$,$\frac{4k}{4+{k}^{2}}$)
∴yM=$\frac{4k}{4+{k}^{2}}$=$\frac{4}{k+\frac{4}{k}}$在(0,2)上单调递增,∴yM∈(0,1)
(3)由题意,kAP•kBP=$\frac{{y}_{1}}{1+{x}_{1}}•\frac{{y}_{1}}{1-{x}_{1}}$=4,
同理kAP•kOM=-4,
∴kOM+kBP=0,
设直线OM:y=k′x,则直线BP:y=-k′(x-1),解得x=$\frac{1}{2}$,
∵kOM+kBP=0,∴直线BP与OM关于直线x=$\frac{1}{2}$对称.
点评 本题考查轨迹方程,考查直线与圆锥曲线的位置关系,考查斜率的计算,属于中档题.

| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
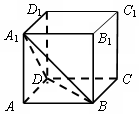 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
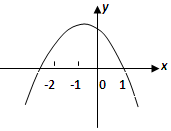 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0