题目内容
O，N，P在△ABC所在平面内，且|
|=|
|=|
|，
+
+
=
，且
•
=
•
=
•
，则点O，N，P依次是△ABC的 心、 心、 心（请按顺序填写）．
| OA |
| OB |
| OC |
| NA |
| NB |
| NC |
| 0 |
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
考点：三角形五心
专题：综合题,平面向量及应用
分析：根据三角形外接圆的性质，结合|
|=|
|=|
|，可得O为△ABC的外心；根据向量加法的平行四边形法则和向量共线定理，可证出N为△ABC的三条中线的交点，得N为△ABC的重心；根据向量数量积的运算性质与向量减法法则，结合
•
=
•
，证出
⊥
，点P在AC边上的高所在直线上．同理可得点P也在AB、BC边上的高所在直线上，因此，P是△ABC三条高所在直线的交点，即得P为△ABC的垂心．
| OA |
| OB |
| OC |
| PA |
| PB |
| PB |
| PC |
| CA |
| PB |
解答：
解：①若|
|=|
|=|
|，则点O到A、B、C三点的距离相等，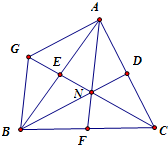
∴O为△ABC的外接圆的圆心，即外心；
②若
+
+
=
，则
+
=-
，
以NA、NB为邻边作平行四边形NAGB，
可得GN、AB的交点E为AB的中点，且E、N、C三点共线．
因此，CE为△ABC的中线．同理可得BN、AN也在△ABC的中线上．
∴点N为△ABC的三条中线的交点，可得N为△ABC的重心；
③若
•
=
•
，
可得（
-
）•
=0，
∴
•
=0，可得
⊥
，点P在AC边上的高所在直线上．
同理可得点P也在AB、BC边上的高所在直线上．
因此，P是△ABC三条高所在直线的交点，即得P为△ABC的垂心．
综上所述，点O、N、P依次是△ABC的外心、重心、垂心．
故答案为：外心、重心、垂心
| OA |
| OB |
| OC |
∴O为△ABC的外接圆的圆心，即外心；
②若
| NA |
| NB |
| NC |
| 0 |
| NA |
| NB |
| NC |
以NA、NB为邻边作平行四边形NAGB，
可得GN、AB的交点E为AB的中点，且E、N、C三点共线．
因此，CE为△ABC的中线．同理可得BN、AN也在△ABC的中线上．
∴点N为△ABC的三条中线的交点，可得N为△ABC的重心；
③若
| PA |
| PB |
| PB |
| PC |
可得（
| PA |
| PC |
| PB |
∴
| CA |
| PB |
| CA |
| PB |
同理可得点P也在AB、BC边上的高所在直线上．
因此，P是△ABC三条高所在直线的交点，即得P为△ABC的垂心．
综上所述，点O、N、P依次是△ABC的外心、重心、垂心．
故答案为：外心、重心、垂心
点评：本题给出三角形中的点满足的向量式，求该点是三角形“五心”中的哪一个．着重考查了向量的加法、减法法则和向量数量积的运算性质等知识，考查了向量在几何中的应用，属于中档题．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
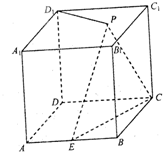在棱长为2的正方体ABCD-A1B1C1D1中，E为棱AB的中点，点P在平面A1B1C1D1内，若D1P⊥平面PCE，试求线段D1P的长．
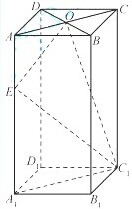如图，长方体ABCD-A1B1C1D1中，底面A1B1C1D1是正方形，E为棱AA1上任意一点，F是CD的中点．