题目内容
7.设函数f(x)=$\frac{1}{2}cos({ωx+φ})$,对任意x∈R都有$f({\frac{π}{3}-x})$=$f({\frac{π}{3}+x})$,若函数g(x)=3sin(ωx+φ)-2,则$g({\frac{π}{3}})$的值为-2.分析 由题意可得函数f(x)的图象关于直线x=$\frac{π}{3}$对称,故f($\frac{π}{3}$)=cos(ωx+φ)=±1,可得sin(ω•$\frac{π}{3}$+φ)=0,从而求得g($\frac{π}{3}$)=3sin(ω•$\frac{π}{3}$+φ)-2的值.
解答 解:由题意可得函数f(x)=$\frac{1}{2}cos({ωx+φ})$的图象关于直线x=$\frac{π}{3}$对称,
故f($\frac{π}{3}$)=cos(ωx+φ)=±1,∴sin(ω•$\frac{π}{3}$+φ)=0,∴g($\frac{π}{3}$)=3sin(ω•$\frac{π}{3}$+φ)-2=-2,
故答案为:-2.
点评 本题主要考查余弦函数的图象的对称性,同角三角函数的基本关系,属于基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
2.某几何体的三视图,如图所示,则该几何体的体积为( )
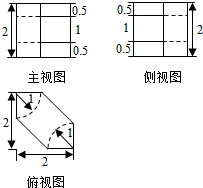

| A. | 7-$\frac{π}{4}$ | B. | 7-$\frac{π}{2}$ | C. | 6-$\frac{π}{2}$ | D. | 6-π |
12.设等比数列{an}的前n项和为Sn,若$\frac{{S}_{6}}{{S}_{3}}$=3,则$\frac{{a}_{11}}{{a}_{2}}$( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
19.已知数列{an}满足an+1=$\left\{\begin{array}{l}2{a_n}({0≤{a_n}<\frac{1}{2}})\\ 2{a_n}-1({\frac{1}{2}≤{a_n}<1})\end{array}$若a1=$\frac{6}{7}$,则a2012的值为( )
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
16.平面α上有不共线三点到平面β的距离相等,则α与β的位置关系为( )
| A. | 平行 | B. | 相交 | C. | 平行或相交 | D. | 垂直 |
 .
. 时,求不等式
时,求不等式 的解集;
的解集; 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围. 在点
在点 处的切线的斜率为
处的切线的斜率为 ,则函数
,则函数 的部分图象可以为( )
的部分图象可以为( )