题目内容
19．等比数列{an}中，a2=2，a5=$\frac{1}{4}$，则a7=（ ）| A． | $\frac{1}{64}$ | B． | $\frac{1}{32}$ | C． | $\frac{1}{16}$ | D． | $\frac{1}{8}$ |
分析 由等比数列的性质可得：${a}_{7}=\frac{{a}_{5}^{2}}{{a}_{2}}$，代入即可得出．
解答 解：由等比数列的性质可得：${a}_{7}=\frac{{a}_{5}^{2}}{{a}_{2}}$=$\frac{（\frac{1}{4}）^{2}}{2}$=$\frac{1}{32}$．
故选：B．
点评 本题考查了等比数列的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
9．已知集合A={-1，1，4}，B={y|y=log2|x|+1，x∈A}，则A∩B=（ ）
| A． | {-1，1，3，4} | B． | {-1，1，3} | C． | {1，3} | D． | {1} |
14．
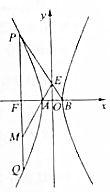已知O为坐标原点，F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，A，B分别为左、右顶点，过点F做x轴的垂线交双曲线于点P，Q，连接PB交y轴于点E，连结AE交QF于点M，若M是线段QF的中点，则双曲线C的离心率为（ ）
已知O为坐标原点，F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点，A，B分别为左、右顶点，过点F做x轴的垂线交双曲线于点P，Q，连接PB交y轴于点E，连结AE交QF于点M，若M是线段QF的中点，则双曲线C的离心率为（ ）| A． | 2 | B． | $\frac{5}{2}$ | C． | 3 | D． | $\frac{7}{2}$ |
11．（理）设θ为直线$x-\sqrt{3}y-1=0$的倾斜角，则$sin（θ+\frac{π}{4}）$=（ ）
| A． | $\frac{{\sqrt{6}-\sqrt{2}}}{4}$ | B． | $\frac{{\sqrt{6}+1}}{4}$ | C． | $\frac{{\sqrt{6}+\sqrt{2}}}{4}$ | D． | $\frac{{\sqrt{2}-\sqrt{6}}}{4}$ |
8．运行如图所示的程序框图，输出的n等于（ ）
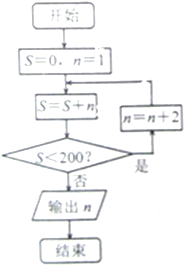
| A． | 30零 | B． | 29 | C． | 28 | D． | 27 |