题目内容
f（x）=
+2x（x＞1），则f（x）的最小值为 ．
| 2 |
| x-1 |
考点：基本不等式在最值问题中的应用
专题：计算题,不等式的解法及应用
分析：先判定x-1＞0，再由f（x）=
+2x=2（
+x-1）+2，根据基本不等式可求得最小值．
| 2 |
| x-1 |
| 1 |
| x-1 |
解答：
解：∵x＞1，∴x-1＞0
∵f（x）=
+2x=2（
+x-1）+2≥4+2=6
当且仅当
=x-1，即x=2时等号成立
∴函数f（x）的最小值为6．
故答案为：6．
∵f（x）=
| 2 |
| x-1 |
| 1 |
| x-1 |
当且仅当
| 1 |
| x-1 |
∴函数f（x）的最小值为6．
故答案为：6．
点评：本题主要考查基本不等式的应用．应用基本不等式时要注意“一正、二定、三相等”的要求．
练习册系列答案
相关题目
执行图的程序框图，若输入的a，b，k分别为1，2，3，则输出的M=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有800名学生参加了这次竞赛．为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表和频率分布直方图，解答下列问题：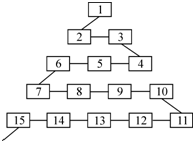
如图是网络工作者经常用来解释网络运作的蛇形模型：数字1出现在第1行；数字2，3出现在第2行；数字6，5，4（从左至右）出现在第3行；数字7，8，9，10出现在第4行；…；依此类推，则下列集合中为空集的是（ ）
| A、{x∈N|x2≤0} |
| B、{x∈R|x2-1=0} |
| C、{x∈R|x2+x+1=0} |
| D、{0} |
有两个等差数列{an}，{bn}，它们的前n项和分别为Sn，Tn，若
=
，则
=（ ）
| an |
| bn |
| 4n+3 |
| n+2 |
| S11 |
| T11 |
A、
| ||
B、
| ||
C、
| ||
D、
|