题目内容
已知
=
,则tanθ=( )
| 1+sinθ+cosθ |
| 1+sinθ-cosθ |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
考点:同角三角函数基本关系的运用
专题:计算题,三角函数的求值
分析:由条件,先求出tan
=2,可得tanθ=
,即可求出结论.
| θ |
| 2 |
2tan
| ||
1-tan2
|
解答:
解:∵
=
,
∴
=
,
∴tan
=2,
∴tanθ=
=-
.
故选:B.
| 1+sinθ+cosθ |
| 1+sinθ-cosθ |
| 1 |
| 2 |
∴
2cos2
| ||||||
2sin2
|
| 1 |
| 2 |
∴tan
| θ |
| 2 |
∴tanθ=
2tan
| ||
1-tan2
|
| 4 |
| 3 |
故选:B.
点评:本题考查二倍角公式,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
离心率e=
是双曲线的两条渐近线互相垂直的( )
| 2 |
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、不充分不必要条件 |
抛物线y=
x2的焦点坐标为( )
| 1 |
| 8 |
| A、(0,2) | ||
B、(0,
| ||
| C、(2,0) | ||
D、(
|
函数f(x)的定义域为R,f(2)=4,对?x∈R,f′(x)>3,则f(x)>3x-2的解集是( )
| A、(-∞,+∞) |
| B、(2,+∞) |
| C、(-∞,2) |
| D、(-2,2) |
在边长为1的等边三角形ABC中,
•
=( )
| AB |
| AC |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
某四面体的三视图如图所示,该四面体的表面积是( )
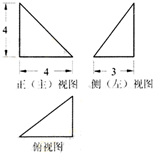

A、40+4
| ||
B、20+2
| ||
C、24+6
| ||
D、48+12
|
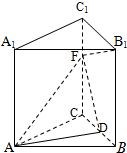 在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.
在直三棱柱ABC-A1B1C1中,AB=AC=AA1=3a,BC=2a,D是BC的中点,F是C1C上一点,且CF=2a.