题目内容
离心率e=
是双曲线的两条渐近线互相垂直的（ ）
| 2 |
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、不充分不必要条件 |
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的性质求出双曲线的渐近线，即可得到结论．
解答：
解：若离心率e=
?双曲线为等轴双曲线?等轴双曲线的渐近线为y=x和y=-x?双曲线渐近线互相垂直，
则离心率e=
是双曲线的两条渐近线互相垂直的充要条件，
故选：C．
| 2 |
则离心率e=
| 2 |
故选：C．
点评：本题主要考查双曲线的性质，根据离心率求出双曲线为等轴双曲线是解决本题的关键．
练习册系列答案
相关题目
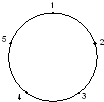如图，圆周上按顺时针方向标有1，2，3，4，5五个点．一只青蛙按顺时针方向绕圆从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则跳两个点．该青蛙从5这点跳起，经2013次跳后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
直线2x-my+1-3m=0，当m变动时，所有直线都通过定点（ ）
A、（-
| ||
B、（
| ||
C、（
| ||
D、（-
|
已知
=
，则tanθ=（ ）
| 1+sinθ+cosθ |
| 1+sinθ-cosθ |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
下列函数中，最小正周期是
的偶函数为（ ）
| π |
| 2 |
| A、y=tan2x | ||
B、y=cos（4x+
| ||
| C、y=2cos22x-1 | ||
| D、y=cos2x |