题目内容
双曲线C的渐近线方程为y=±x，则该双曲线的离心率为 ．
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据双曲线的渐近线得到双曲线的方程，即可得到结论．
解答：
解：∵双曲线C的渐近线方程为y=±x，
∴双曲线C为等轴双曲线，
即a=b，则c=
=
a，
则双曲线的离心率为e=
，
故答案为：
∴双曲线C为等轴双曲线，
即a=b，则c=
| a2+b2 |
| 2 |
则双曲线的离心率为e=
| 2 |
故答案为：
| 2 |
点评：本题主要考查双曲线的离心率的计算，根据等轴双曲线的性质是解决本题的关键．
练习册系列答案
相关题目
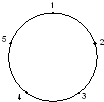如图，圆周上按顺时针方向标有1，2，3，4，5五个点．一只青蛙按顺时针方向绕圆从一个点跳到另一点．若它停在奇数点上，则下一次只能跳一个点；若停在偶数点上，则跳两个点．该青蛙从5这点跳起，经2013次跳后它将停在的点是（ ）| A、1 | B、2 | C、3 | D、4 |
已知
=
，则tanθ=（ ）
| 1+sinθ+cosθ |
| 1+sinθ-cosθ |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
归纳推理是（ ）
| A、特殊到一般的推理 |
| B、特殊到特殊的推理 |
| C、一般到特殊的推理 |
| D、一般到一般的推理 |