题目内容
某四面体的三视图如图所示,该四面体的表面积是( )
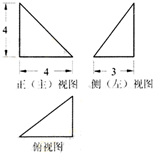

A、40+4
| ||
B、20+2
| ||
C、24+6
| ||
D、48+12
|
考点:由三视图求面积、体积
专题:常规题型
分析:四面体即为三棱锥,想象其形状与方位,如底面与侧面的形状,顶点位置等,再探求各边的长度,从而得各面的面积,即可得表面积.
解答:
解:把四面体看作是三棱锥,由正、侧视图知,
三棱锥的顶点在上,底面在下,且高SA=4,△SAB,△SAC均为直角三角形,
由俯视图知,△ABC为直角三角形,底面直角边AB=4,又由侧视图得,直角边BC=3,
由此可画出此四面体的直观图,如右图所示.
从而S△ABC=
AB•BC=
×4×3=6,
S△SAB=
AB•SA=
×4×4=8,
S△SAC=
AC•SA=
•SA=10.
由SA⊥平面ABC知,SA⊥BC,
又BC⊥AB,∴BC⊥平面SAB,∴BC⊥SB,
∴S△SBC=
BC•SB=
BC•
=6
.
∴四面体的表面积为S△ABC+S△SAB+S△SAC+S△SBC=6+8+10+6
=24+6
.
故选C.
三棱锥的顶点在上,底面在下,且高SA=4,△SAB,△SAC均为直角三角形,
由俯视图知,△ABC为直角三角形,底面直角边AB=4,又由侧视图得,直角边BC=3,

由此可画出此四面体的直观图,如右图所示.
从而S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S△SAB=
| 1 |
| 2 |
| 1 |
| 2 |
S△SAC=
| 1 |
| 2 |
| 1 |
| 2 |
| AB2+BC2 |
由SA⊥平面ABC知,SA⊥BC,
又BC⊥AB,∴BC⊥平面SAB,∴BC⊥SB,
∴S△SBC=
| 1 |
| 2 |
| 1 |
| 2 |
| SA2+AB2 |
| 2 |
∴四面体的表面积为S△ABC+S△SAB+S△SAC+S△SBC=6+8+10+6
| 2 |
| 2 |
故选C.
点评:本题属于已知三视图求原几何体的表面积问题,这是高考中的一种很常见的题型,应引起重视.可以考虑以下几方面:
(1)从某个视图入手,找到突破口,通过想象、猜测几何体某面或某个部分的形状及方位;
(2)结合其他两个视图,确定整个几何体的形状与摆放的方位;
(3)以左右为长,前后为宽,上下为高,寻找已知三视图中边的尺寸、角的大小与几何体长,宽,高的联系;
(4)画出几何体的直观图,探讨面积、体积或其它点、线、面的位置关系问题.
(1)从某个视图入手,找到突破口,通过想象、猜测几何体某面或某个部分的形状及方位;
(2)结合其他两个视图,确定整个几何体的形状与摆放的方位;
(3)以左右为长,前后为宽,上下为高,寻找已知三视图中边的尺寸、角的大小与几何体长,宽,高的联系;
(4)画出几何体的直观图,探讨面积、体积或其它点、线、面的位置关系问题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知
=
,则tanθ=( )
| 1+sinθ+cosθ |
| 1+sinθ-cosθ |
| 1 |
| 2 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
下列函数中,最小正周期是
的偶函数为( )
| π |
| 2 |
| A、y=tan2x | ||
B、y=cos(4x+
| ||
| C、y=2cos22x-1 | ||
| D、y=cos2x |
 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列命题:①平面A′FG⊥平面ABC;
②BC∥平面A′DE;
③三棱锥A′-DEF的体积最大值为
| 1 |
| 64 |
④存在某个位置,使得DF与A′E垂直.
其中正确的命题是( )
| A、② | B、②③ |
| C、①②③ | D、①②③④ |
双曲线两条渐近线的夹角为60°,该双曲线的离心率为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
归纳推理是( )
| A、特殊到一般的推理 |
| B、特殊到特殊的推理 |
| C、一般到特殊的推理 |
| D、一般到一般的推理 |
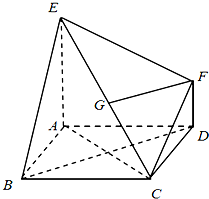 如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.
如图,已知多面体EABCDF的底面ABCD是正方形,EA⊥底面ABCD,FD∥EA,且EA=2FD.