题目内容
已知f′(x)是函数f(x)的导函数,将y=f(x)和y=f′(x)的图象画在同一个直角坐标系中,不可能正确的是( )
A、 |
B、 |
C、 |
D、 |
考点:函数的单调性与导数的关系
专题:导数的概念及应用
分析:本题可以考虑排除法,容易看出选项D不正确,因为D的图象,在整个定义域内,不具有单调性,但y=f(x)和y=f′(x)在整个定义域内具有完全相同的走势,不具有这样的函数.
解答:
解:不可能正确的是D.
因为把上面的作为函数:在最左边单调递增,其导数应为大于0,但是其导函数的值小于0,故不正确;
同样把下面的作为函数,中间一段是减函数,导函数应该小于0,也不正确.因此D不正确.
故选:D.
因为把上面的作为函数:在最左边单调递增,其导数应为大于0,但是其导函数的值小于0,故不正确;
同样把下面的作为函数,中间一段是减函数,导函数应该小于0,也不正确.因此D不正确.
故选:D.
点评:本题考查导数与函数单调性的关系,属于一道基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
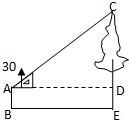 如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )
如图,小明利用有一个锐角是30°的三角板测量一棵树的高度,已知他与树之间的水平距离BE为5m,AB为1.5m(即小明的眼睛距地面的距离),那么这棵树高是( )A、(
| ||||||
B、(5
| ||||||
C、
| ||||||
| D、4m |
已知
,
均为单位向量,它们的夹角为60°,那么|
+2
|等于( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、4 |
已知0<a<1,则函数y=|logax|-a|x|零点的个数是( )
| A、1个 | B、2个 |
| C、3个 | D、1个或2个或3个 |
在△ABC中,“sin(A-B)cosB+cos(A-B)sinB≥1”是“△ABC是直角三角形”的( )
| A、充分必要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
 如图,在半径为
如图,在半径为