题目内容
已知两直线l1:mx+8y+n=0和l2:2x+my-1=0,若l1⊥l2且l1在y轴上的截距为-1,则m,n的值分别为( )
| A、2,7 | B、0,8 |
| C、-1,2 | D、0,-8 |
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:由两直线垂直,x,y的系数积之和为0,能求出m=0,再由l1在y轴上的截距为-1,知直线l1过点(0,-1),由此能求出n.
解答:
解:∵两直线l1:mx+8y+n=0和l2:2x+my-1=0,
l1⊥l2且l1在y轴上的截距为-1,
∴
,
解得m=0,n=8.
故选:B.
l1⊥l2且l1在y轴上的截距为-1,
∴
|
解得m=0,n=8.
故选:B.
点评:本题考查直线中参数值的求法,是基础题,解题时要注意两直线垂直的性质的合理运用.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
(x-
)8的二项展开式中,x2的系数是( )
| 1 | ||
|
| A、70 | B、-70 |
| C、28 | D、-28 |
如图所示,直线l1,l2,l3的斜率分别为k1,k2,k3,则( )
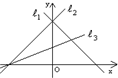

| A、k1<k2<k3 |
| B、k3<k1<k2 |
| C、k1<k3<k2 |
| D、k3<k2<k1 |
已知全集U=R,A={x|2x<1},B={x|y=lg(2-x)},则(∁UA)∩B=( )
| A、(1,2] |
| B、(1,2) |
| C、(0,2] |
| D、[0,2) |
已知函数f(x)=x2+2bx的图象在点O(0,0)处的切线l与直线x-y+3=0平行,若数列{
}的前n项和为Sn,则S2014=( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|