题目内容
已知实数x,y,z,给出下列命题:
①若x>1,y>1,且lnx,1,4lny成等比数列,则xy有最小值e;
②若x,y,z为正实数,且满足x2+y2+z2=1,则
+
+
的最小值为9;
③若x和y为正数,a=x+y,b=
,c=2
,则a、b、c可作三角形的三边;
④若关于x方程
=kx2有4个不同的实数解,则k∈(1,+∞).
其中正确命题的序号为: (写出所有正确结论的编号)
①若x>1,y>1,且lnx,1,4lny成等比数列,则xy有最小值e;
②若x,y,z为正实数,且满足x2+y2+z2=1,则
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| z2 |
③若x和y为正数,a=x+y,b=
| x2+xy+y2 |
| xy |
④若关于x方程
| |x| |
| x+4 |
其中正确命题的序号为:
考点:命题的真假判断与应用
专题:阅读型
分析:必须对选项一一加以判断,①运用等比数列的性质和基本不等式的知识来判断;②运用基本不等式的知识来判断;③由三角形的任意两边之和大于第三边来判断;④对x讨论,分x=0,x>0,x<0,去绝对值并结合图象即可判断.
解答:
解:①若x>1,y>1,且lnx,1,4lny成等比数列,则lnx>0,lny>0,4lnx•lny=1,故lnx+lny≥2
=2×
=1,即ln(xy)≥1,xy≥e,当且仅当x=y=
,取最小值e,故①正确;
②若x,y,z为正实数,且满足x2+y2+z2=1,则
+
+
=
+
+
=3+(
+
)+(
+
)+(
+
)≥3+2+2+2=9,当且仅当x=y=z时,取最小值9.故②正确;
③若x和y为正数,a=x+y,b=
,c=2
,则a>0,b>0,c>0,a≥c,a>b,则a+b>c,a+c>b,又(b+c)2=b2+c2+2bc=x2+y2+5xy+2bc>a2,即b+c>a,故a、b、c可作三角形的三边,故③正确;
④关于x的方程
=kx2,当x=0时,显然成立,
由于有4个不同的实数解,则还有3个非零解,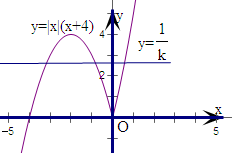
当x>0时,方程可化为x(x+4)=
,
当x<0时,方程可化为-x(x+4)=
,
画出函数y=|x|(x+4)(x≠0且x≠-4)的图象,
画出y=
的图象,将其平移观察有三个交点的情况得,
0<
<4,即k>
.故④不正确.
故答案为:①②③.
| lnx•lny |
| 1 |
| 2 |
| e |
②若x,y,z为正实数,且满足x2+y2+z2=1,则
| 1 |
| x2 |
| 1 |
| y2 |
| 1 |
| z2 |
| x2+y2+z2 |
| x2 |
| x2+y2+z2 |
| y2 |
| x2+y2+z2 |
| z2 |
=3+(
| y2 |
| x2 |
| x2 |
| y2 |
| z2 |
| x2 |
| x2 |
| z2 |
| z2 |
| y2 |
| y2 |
| z2 |
③若x和y为正数,a=x+y,b=
| x2+xy+y2 |
| xy |
④关于x的方程
| |x| |
| x+4 |
由于有4个不同的实数解,则还有3个非零解,

当x>0时,方程可化为x(x+4)=
| 1 |
| k |
当x<0时,方程可化为-x(x+4)=
| 1 |
| k |
画出函数y=|x|(x+4)(x≠0且x≠-4)的图象,
画出y=
| 1 |
| k |
0<
| 1 |
| k |
| 1 |
| 4 |
故答案为:①②③.
点评:本题以命题的真假为载体考查等比数列的性质和基本不等式的运用求最值,注意等号成立的条件,考查不等式的基本性质,同时还考查方程解的个数问题转化为两函数图象交点的个数,属于综合题.

练习册系列答案
相关题目
已知函数y=f(x)是定义在(-2,2)的奇函数,当x∈(0,2)时,f(x)=2x-1,则f(log2
)的值为( )
| 1 |
| 3 |
A、
| |||
B、-
| |||
| C、2 | |||
| D、-2 |
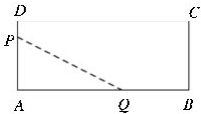 如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为
如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为