题目内容
已知向量
=(2,1),
=(-1,2),若
,
在向量
上的投影相等,且(
-
)•(
-
)=-
,则向量
的坐标为 .
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| c |
| b |
| 5 |
| 2 |
| c |
考点:平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:根据向量的投影的定义域向量数量积之间的关系,建立方程,即可求出向量
的坐标.
| c |
解答:
解:设向量
的坐标为(x,y),
若
,
在向量
上的投影相等,
则
=
,即
•
=
•
,
∴
•(
-
)=0,即(x,y)•(3,-1)=3x-y=0,①
∵(
-
)•(
-
)=-
,
∴(x-2,y-1)•(x+1,y-2)=-
,
∴(x-2)(x+1)+(y-1)(y-2)=-
,②
将y=3x代入②得,
即4x2-4x+1=0,
即(2x-1)2=0,
解得x=
,y=
,
即向量
的坐标为(
,
),
故答案为:(
,
).
| c |
若
| a |
| b |
| c |
则
| ||||
|
|
| ||||
|
|
| a |
| c |
| b |
| c |
∴
| c |
| a |
| b |
∵(
| c |
| a |
| c |
| b |
| 5 |
| 2 |
∴(x-2,y-1)•(x+1,y-2)=-
| 5 |
| 2 |
∴(x-2)(x+1)+(y-1)(y-2)=-
| 5 |
| 2 |
将y=3x代入②得,
即4x2-4x+1=0,
即(2x-1)2=0,
解得x=
| 1 |
| 2 |
| 3 |
| 2 |
即向量
| c |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为:(
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题主要考查向量的数量积的运算,要求熟练掌握投影的概念以及向量的坐标公式.

练习册系列答案
相关题目
已知直线l:y=x+b,圆x2+y2=4上恰有3个点到直线l的距离都等于1,则b=( )
A、
| ||
B、-
| ||
C、±
| ||
| D、±2 |
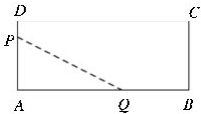 如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为
如图,有一矩形地块ABCD,其相邻边长为20m和50m,现要在它的短边与长边上各取一点P与Q,用周长为80m的篱笆围出一块直角三角形的花园,则围出部分的最大面积为