题目内容
已知等差数列{an}（n∈N*）的公差为3，a1=-1，前n项和为Sn，则
的数值是 ．
| lim |
| n→∞ |
| nan |
| Sn |
考点：等差数列的前n项和,极限及其运算
专题：等差数列与等比数列
分析：利用等差数列的性质求出
=
=
，由此能求出
的值．
| nan |
| Sn |
| 3n2-4n | ||||
|
| 3n-4 | ||||
|
| lim |
| n→∞ |
| nan |
| Sn |
解答：
解：∵等差数列{an}（n∈N*）的公差为3，
a1=-1，前n项和为Sn，
∴an=-1+（n-1）×3=3n-4，
Sn=-n+
×3=
n2-
n，
∴
=
=
，
∴
=
=2．
故答案为：2．
a1=-1，前n项和为Sn，
∴an=-1+（n-1）×3=3n-4，
Sn=-n+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
∴
| nan |
| Sn |
| 3n2-4n | ||||
|
| 3n-4 | ||||
|
∴
| lim |
| n→∞ |
| nan |
| Sn |
| lim |
| n→∞ |
| 3n-4 | ||||
|
故答案为：2．
点评：本题考查极限的求法，是基础题，解题时要熟练掌握等差数列的通项公式和前n项和公式的灵活运用．
练习册系列答案
相关题目
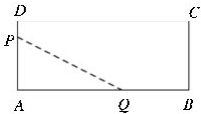如图，有一矩形地块ABCD，其相邻边长为20m和50m，现要在它的短边与长边上各取一点P与Q，用周长为80m的篱笆围出一块直角三角形的花园，则围出部分的最大面积为