题目内容
13.(1)已知△ABC三个顶点坐标为A(2,-1),B(2,2),C(4,1),求三角形AC边上的中线所在直线方程;(2)倾斜角为60°且与直线5x-y+2=0有相同纵截距的直线方程.
分析 (1)由中点坐标公式求出AC的中点坐标,再由直线方程的两点式求得三角形AC边上的中线所在直线方程;
(2)化直线系方程的一般式为斜截式,得到已知直线的纵截距,再由斜率等于倾斜角的正切值求得所求直线的斜率,代入直线方程的点斜式得答案.
解答 解:(1)由A(2,-1),C(4,1),得AC的中点坐标为(3,0),
又B(2,2),由直线方程的两点式得$\frac{y-0}{2-0}=\frac{x-3}{2-3}$,即2x+y-6=0.
∴三角形AC边上的中线所在直线方程为2x+y-6=0;
(2)由直线5x-y+2=0,得y=5x+2,∴直线5x-y+2=0的纵截距为2,
由k=tan60°=$\sqrt{3}$,
可得倾斜角为60°且与直线5x-y+2=0有相同纵截距的直线方程为y=$\sqrt{3}x+2$.
点评 本题考查直线的一般式方程,考查了直线方程的两点式与斜截式,是基础题.

练习册系列答案
相关题目
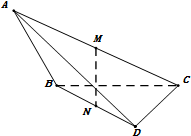 如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.
如图,在三棱锥A-BCD中,二面角A-BC-D的大小为$\frac{π}{4}$,AB⊥BC,DC⊥BC,M,N分别为AC,BD的中点,已知AB=$\sqrt{2}$,BC=CD=1.