题目内容
设函数f(x)=
,若对任意给定的t∈(1,+∞),都存在唯一的x∈R,满足f(f(x))=2a2t2+at,则正实数a的最小值是( )
|
| A、2 | ||
B、
| ||
C、
| ||
D、
|
考点:分段函数的应用
专题:函数的性质及应用
分析:此题的突破口在于如何才会存在唯一的x满足条件,结合f(x)的值域范围或者图象,易知只有在f(x)的自变量与因变量存在一一对应的关系时,即只有当f(x)>2时,才会存在一一对应.
解答:
解:根据f(x)的函数,我们易得出其值域为:R,
又∵f(x)=2x,(x≤0)时,值域为(0,1];
f(x)=log2x,(x>0)时,其值域为R,
∴可以看出f(x)的值域为(0,1]上有两个解,
要想f(f(x))=2a2t2+at,在t∈(1,+∞)上只有唯一的x∈R满足,
必有f(f(x))>1 (因为2a2t2+at>0),
所以:f(x)>2,
解得:x>4,
当 x>4时,x与f(f(x))存在一一对应的关系,
∴2a2t2+at>1,t∈(1,+∞),且a>0,
所以有:(2at-1)(at+1)>0,
解得:t>
或者t<-
(舍去),
∴
≤1,
∴a≥
,
故选:B
又∵f(x)=2x,(x≤0)时,值域为(0,1];
f(x)=log2x,(x>0)时,其值域为R,
∴可以看出f(x)的值域为(0,1]上有两个解,
要想f(f(x))=2a2t2+at,在t∈(1,+∞)上只有唯一的x∈R满足,
必有f(f(x))>1 (因为2a2t2+at>0),
所以:f(x)>2,
解得:x>4,
当 x>4时,x与f(f(x))存在一一对应的关系,
∴2a2t2+at>1,t∈(1,+∞),且a>0,
所以有:(2at-1)(at+1)>0,
解得:t>
| 1 |
| 2a |
| 1 |
| a |
∴
| 1 |
| 2a |
∴a≥
| 1 |
| 2 |
故选:B
点评:本题主要考查了分段函数的应用,本题关键是可以把2a2t2+at当作是一个数,然后在确定数的大小后再把它作为一个关于t的函数.

练习册系列答案
相关题目
若一个等差数列首项为0,公差为2,则这个等差数列的前20项之和为( )
| A、360 | B、370 |
| C、380 | D、390 |
设i为虚数单位,则复数z=
在复平面内对应的点所在的象限是( )
| 1+i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知定义在R上的函数f(x)=
若直线y=a与函数f(x)的图象恰有两个公共点,则实数a的取值范围是( )
|
| A、(0,2) |
| B、[0,2) |
| C、(0,2] |
| D、[1,2] |
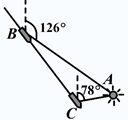 如图,货轮在海上以35nmile/h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为148°的方向航行.为了确定船位,在B点观察灯塔A的方位角是126°,航行半小时后到达C点,观察灯塔A的方位角是78°.求货轮到达C点时与灯塔A的距离(精确到0.01nmile).
如图,货轮在海上以35nmile/h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为148°的方向航行.为了确定船位,在B点观察灯塔A的方位角是126°,航行半小时后到达C点,观察灯塔A的方位角是78°.求货轮到达C点时与灯塔A的距离(精确到0.01nmile).