Question

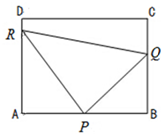如图，在矩形ABCD中，AB=2，AD=

3

，P是AB的中点，该矩形有一内接Rt△PQR，P为直角顶点，Q、R分别落在线段BC和线段AD上，记Rt△PQR的面积为S．
（Ⅰ）设∠BPQ为α，将S表示成α的函数关系式，并求S的最大值；
（Ⅱ）设BQ=x，将S表示成x的函数关系式．并求S的最小值．

Answer 1

考点：基本不等式在最值问题中的应用

专题：综合题,导数的综合应用

分析：（Ⅰ）由题意表示出S=

1

2

PR•PQ=

1

2

•

1

cosα

•

1

sinα

=

1

sin2α

，从而求f（α）的最大值；
（Ⅱ）设BQ=x，BP=1，S=

1

2

1+x2

•

1+ 1 x2

=

1

2

x2+ 1 x2 +2

，利用换元法求函数的最值．

解答： 解：（Ⅰ）由图知，在Rt△PBQ中，PQ=

1

cosα

；在Rt△PAR中，RP=

1

sinα

．
因为∠RPQ为直角，所以S=

1

2

PR•PQ=

1

2

•

1

cosα

•

1

sinα

=

1

sin2α

．
又R，Q分别在线段AD、BC上，所以

π

6

≤α≤

π

3

，∴

π

3

≤2α≤

2π

3

，∴sin2α∈[

3

2

，1]，∴当2α=

π

3

或

2π

3

时，(sin2α)min=

3

2

，∴Smax=

2 3

3

．
因此S=

1

sin2α

(

π

6

≤α≤

π

3

)，S=f（α）的最大值为

2

3

3

．…（7分）
（Ⅱ）∵BQ=x，BP=1，∴PQ=

1+x2

，
又∵△PBQ∽△RAP，∴

BQ

BP

=

AP

AR

，∴AR=

1

x

，∴PR=

1+ 1 x2

，
∴S=

1

2

1+x2

•

1+ 1 x2

=

1

2

x2+ 1 x2 +2

．
由于R，Q在线段AD，BC上，∴

3

3

≤x≤

3

，∴S=

1

2

x2+ 1 x2 +2

（

3

3

≤x≤

3

）．
令t=x2，则

1

3

≤t≤3，S=

1

2

t+ 1 t +2

(

1

3

≤t≤3)，
∵函数y=t+

1

t

在[

1

3

，1]单调递减，在[1，3]单调递增．
∴当t=1时，y达到最小值2．∴g(x)min=

1

2

2+2

=1．…（14分）

点评：本题考查了函数的解析式的求法，函数单调性的判断与应用，同时考查了函数的最值，属于中档题．