题目内容
△ABC的三个内角A,B,C所对的边分别为a,b,c,a=1,B=45°,向量
=(-1,1),
=(cosBcosC,sinBsinC-
,且
⊥
,
(Ⅰ)求A的大小;
(Ⅱ)求△ABC的面积.
| m |
| n |
| ||
| 2 |
| m |
| n |
(Ⅰ)求A的大小;
(Ⅱ)求△ABC的面积.
考点:正弦定理,余弦定理
专题:解三角形
分析:(I)由
⊥
,利用两个向量垂直的性质,两个向量的数量积公式求得cos(B+C)=-
,再根据cos(B+C)=-cosA,求得A的值.
(II)由条件求得C=105°,利用两角和的正弦公式求得cos105°的值,再利用正弦定理求得c的值,可得△ABC的面积
ac•sinB的值.
| m |
| n |
| ||
| 2 |
(II)由条件求得C=105°,利用两角和的正弦公式求得cos105°的值,再利用正弦定理求得c的值,可得△ABC的面积
| 1 |
| 2 |
解答:
解:(I)∵且
⊥
,∴
•
=-cosBcosC+sinBsinC-
=0,即cosBcosC-sinBsinC=-
,∴cos(B+C)=-
.
∵A+B+C=180°,∴cos(B+C)=-cosA,∴cosA=
,所以A=30°.
(II)∵A=30°,a=1,B=45°,∴C=105°.
又sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
.
由正弦定理得c=
=
=
,
∴S△ABC=
acsinB=
×1×
×
=
.
| m |
| n |
| m |
| n |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∵A+B+C=180°,∴cos(B+C)=-cosA,∴cosA=
| ||
| 2 |
(II)∵A=30°,a=1,B=45°,∴C=105°.
又sin105°=sin(60°+45°)=sin60°cos45°+cos60°sin45°=
| ||||
| 4 |
由正弦定理得c=
| asinC |
| sinA |
| 1•sin105° |
| sin30° |
| ||||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||||
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:本题主要考查两个向量垂直的性质,两个向量的数量积公式,以及正弦定理、两角和的正弦公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
将函数f(x)=sinx-
cosx的图象向左平移m(m>0)个单位,若所得图象对应的函数为偶函数,则m的最小值是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
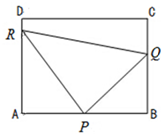 如图,在矩形ABCD中,AB=2,AD=
如图,在矩形ABCD中,AB=2,AD=