题目内容
已知a2、a5是方程x2-12x+27=0的两根,数列{an}是递增的等差数列,数列{bn}的前n项和为Sn,且Sn=1-
bn(n∈N+).
(1)求数列{an},{bn}的通项公式;
(2)记cn=anbn,求数列{cn}的前n项和Tn.
| 1 |
| 2 |
(1)求数列{an},{bn}的通项公式;
(2)记cn=anbn,求数列{cn}的前n项和Tn.
考点:数列的求和,数列的应用
专题:等差数列与等比数列
分析:(1)由于a2、a5是方程x2-12x+27=0的两根,数列{an}是递增的等差数列,可得a2=3,a5=9,利用等差数列的通项公式即可得出an.
对于数列{bn},Sn=1-
bn(n∈N+).当n=1时,b1=1-
b1,解得b1.当n≥2时,bn=Sn-Sn-1,利用等比数列的通项公式可得bn.
(2)cn=anbn=
=
,利用“错位相减法”与等比数列的前n项和公式即可得出.
对于数列{bn},Sn=1-
| 1 |
| 2 |
| 1 |
| 2 |
(2)cn=anbn=
| 2(2n-1) |
| 3n |
| 4n-2 |
| 3n |
解答:
解:(1)解方程x2-12x+27=0,可得x=3或9,∵a2、a5是方程x2-12x+27=0的两根,数列{an}是递增的等差数列,∴a2=3,a5=9,
设公差为d,则
,解得a1=1,d=2,∴an=1+2(n-1)=2n-1.
对于数列{bn},Sn=1-
bn(n∈N+).当n=1时,b1=1-
b1,解得b1=
.当n≥2时,bn=Sn-Sn-1=(1-
bn)-(1-
bn-1),化为bn=
bn-1,因此数列{bn}是等比数列,∴bn=
×(
)n-1=
.(2)cn=anbn=
=
,
∴数列{cn}的前n项和Tn=
+
+
+…+
+
,∴3Tn=2+
+
+…+
,两式相减可得:2Tn=2+
+
+
-
=
-2-
=4-
,∴Tn=2-
.
设公差为d,则
|
对于数列{bn},Sn=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3n |
| 2(2n-1) |
| 3n |
| 4n-2 |
| 3n |
∴数列{cn}的前n项和Tn=
| 2 |
| 3 |
| 6 |
| 32 |
| 10 |
| 33 |
| 4(n-1)-2 |
| 3n-1 |
| 4n-2 |
| 3n |
| 6 |
| 3 |
| 10 |
| 32 |
| 4n-2 |
| 3n-1 |
| 4 |
| 3 |
| 4 |
| 32 |
| 4 |
| 3n-1 |
| 4n-2 |
| 3n |
4(1-
| ||
1-
|
| 4n-2 |
| 3n |
| 4n+4 |
| 3n |
| 2n+2 |
| 3n |
点评:本题考查了“错位相减法”、等差数列与等比数列的通项公式及前n项和公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知 f(x)=|lgx|,若0<a<1<b且f(a)=f(b),则log2(1+ab)的值为( )
| A、0 | B、1 | C、-1 | D、不确定 |
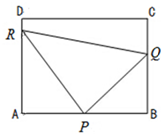 如图,在矩形ABCD中,AB=2,AD=
如图,在矩形ABCD中,AB=2,AD=