题目内容
(1)求函数y=
+
的定义域;
(2)求函数y=-x2+4x-2,x∈[0,3)的最值.
| 1 |
| 2-|x| |
| x2-1 |
(2)求函数y=-x2+4x-2,x∈[0,3)的最值.
考点:二次函数的性质,函数的定义域及其求法
专题:函数的性质及应用
分析:本题(1)根据分式的分母不为0,偶次根式的被开方数非负,得到自变量满足的条件,解不等式,得到函数的定义域;(2)对二次函数进行配方、画图,根据图象特征,得到函数的最值,得到本题结论.
解答:
解:(1)要使原式有意义,则
,
∴
,
∴该函数的定义域为(-∞,-2)∪(-2,-1)∪(1,2)∪(2,+∞).

(2)原式化为y=-(x-2)2+2,x∈[0,3),
由图可知:
当x=2时,ymax=2,
当x=0时,ymin=-2,
故该函数的最大值为2,最小值为-2.
|
∴
|
∴该函数的定义域为(-∞,-2)∪(-2,-1)∪(1,2)∪(2,+∞).

(2)原式化为y=-(x-2)2+2,x∈[0,3),
由图可知:
当x=2时,ymax=2,
当x=0时,ymin=-2,
故该函数的最大值为2,最小值为-2.
点评:本题考查了二次函数的图象与性质,本题难度不大,属于基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
| ∫ | 1 -1 |
| A、0 | B、2sin1 |
| C、2cos1 | D、2 |
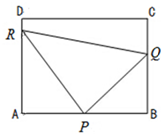 如图,在矩形ABCD中,AB=2,AD=
如图,在矩形ABCD中,AB=2,AD=