题目内容
已知函数f(x)=|x-1|+|x-4|-a,a∈R.
(1)当a=-3,求f(x)≥9的解集;
(2)当f(x)>0在定义域R上恒成立时,求实数a的取值范围.
(1)当a=-3,求f(x)≥9的解集;
(2)当f(x)>0在定义域R上恒成立时,求实数a的取值范围.
考点:函数恒成立问题,带绝对值的函数
专题:不等式的解法及应用
分析:(1)分x<1时、1≤x≤4时和x>4时3种情况加以讨论,分别得到f(x)的表达式,再解不等式f(x)≥9,最后综合可得所求的解集;
(2)f(x)>0可化为|x-1|+|x-4|≥a,故把f(x)>0在定义域R上恒成立转化为|x-1|+|x-4|≥a在定义域R上恒成立,利用求最值解决.
(2)f(x)>0可化为|x-1|+|x-4|≥a,故把f(x)>0在定义域R上恒成立转化为|x-1|+|x-4|≥a在定义域R上恒成立,利用求最值解决.
解答:
解:(1)由于a=-3,∴f(x)=|x-1|+|x-4|-(-3)≥9,
∴|x-1|+|x-4|≥6
当x<1时,|x-1|+|x-4|=1-x+4-x=-2x+5≥6,解得x≤-
;
当1≤x≤4时,|x-1|+|x-4|=x-1+4-x=3≥6,解集为∅;
当x>4时,|x-1|+|x-4|=x-1+x-4=2x-5≥6,解得x≥
;
综上所述,原不等式的解集为{x|x≤-
,或x≥
}.
(2)f(x)>0可化为|x-1|+|x-4|≥a,
∴f(x)>0在定义域R上恒成立也就是|x-1|+|x-4|≥a在定义域R上恒成立,
∵|x-1|+|x-4|≥|(x-1)-(x-4)|=3,
∴要使|x-1|+|x-4|≥a在定义域R上恒成立,只要使3≥a即可,∴a≤3,
∴a的取值范围是(-∞,3)
∴|x-1|+|x-4|≥6
当x<1时,|x-1|+|x-4|=1-x+4-x=-2x+5≥6,解得x≤-
| 1 |
| 2 |
当1≤x≤4时,|x-1|+|x-4|=x-1+4-x=3≥6,解集为∅;
当x>4时,|x-1|+|x-4|=x-1+x-4=2x-5≥6,解得x≥
| 11 |
| 2 |
综上所述,原不等式的解集为{x|x≤-
| 1 |
| 2 |
| 11 |
| 2 |
(2)f(x)>0可化为|x-1|+|x-4|≥a,
∴f(x)>0在定义域R上恒成立也就是|x-1|+|x-4|≥a在定义域R上恒成立,
∵|x-1|+|x-4|≥|(x-1)-(x-4)|=3,
∴要使|x-1|+|x-4|≥a在定义域R上恒成立,只要使3≥a即可,∴a≤3,
∴a的取值范围是(-∞,3)
点评:本题给出含有绝对值的函数,解关于x的不等式,着重考查了绝对值的含义、不等式的解法和不等式恒成立的问题,属于中档题.

练习册系列答案
相关题目
在空间四边形ABCD中,AB、BC、CD、DA上分别取E、F、G、H四点,如果EH、FG交于一点P,则( )
| A、P一定在直线BD上 |
| B、P一定在直线AC上 |
| C、P在直线AC或BD上 |
| D、P既不在直线BD上,也不在AC上 |
(x
-y
)6的展开式中x4y5的系数为( )
| y |
| x |
| A、20 | B、-20 |
| C、-15 | D、15 |
 如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=P,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3.
如图,在四棱锥P-ABCD中,BC⊥平面PAB,且PA=P,O是AB的中点,底面ABCD是直角梯形,AD∥BC,BC=1,AB=2,AD=3.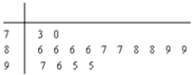 某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):
某电视台组织部分记者,用“10分制”随机调查某社区居民的幸福指数,现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福指数的得分(以小数点前的一位数字为茎,小数点后的一位数字为叶):